コンジョイント分析という商品分析方法を聞いたことがあるでしょうか？ 言葉自体を聞いたことがあっても、コンジョイント分析とは何なのか、使用する場面はいつか、または使い方がよく分からないという方はいるでしょう。 今回はそのような方のために、コンジョイント分析の定義から用途、具体的な分析の手順までを解説致します。

コンジョイント分析とは

コンジョイント分析は、回答者に開発している商品全体を評価をしてもらい、商品の各要素がどのくらい商品全体の評価に影響を与えているのかを明らかにできるのが特徴的な分析方法です。そのため、商品開発を考える際に使われます。

コンジョイント分析を使うと、複数の要素を持つ商品アイデアがあったとき、どの商品アイデアが一番消費者に好まれるか調べることができます。

例えば自動車を購入する際、

1. 100万円で燃費が良く、無名デザイナーＡが手掛けた車
2. 100万円で燃費が悪く、有名デザイナーＢが手掛けた車
3. 150万円で燃費が良く、有名デザイナーＢが手掛けた車
4. 150万円で燃費が悪く、無名デザイナーＡが手掛けた車

これらの選択肢があったとき、あなたならどれを選ぶでしょうか？

コンジョイント分析では、このように複数の要素を同時に比較してもらうことにより、自動車購入において消費者が重要視しているのが、価格なのか、燃費なのか、デザインなのかといった要素の軽重を明らかにすることができます。

単に、消費者に個々の要素について質問を積み重ねると「高品質でなるべく安い製品が良い」という当たり前の答えしか得られないのに対し、コンジョイント分析を使えば要因に優劣がつけられ、効率的で効果的な調査票の作成が可能になるのです。

コンジョイント分析の特徴

コンジョイント分析は、事前に一定のルールに則って商品を構成することを前提としています。
ルールに則って作られた商品に対して、回答者から全体の評価をもらうだけで、どの要素がどのくらい重要視されて選ばれているのかを数値化することができます。

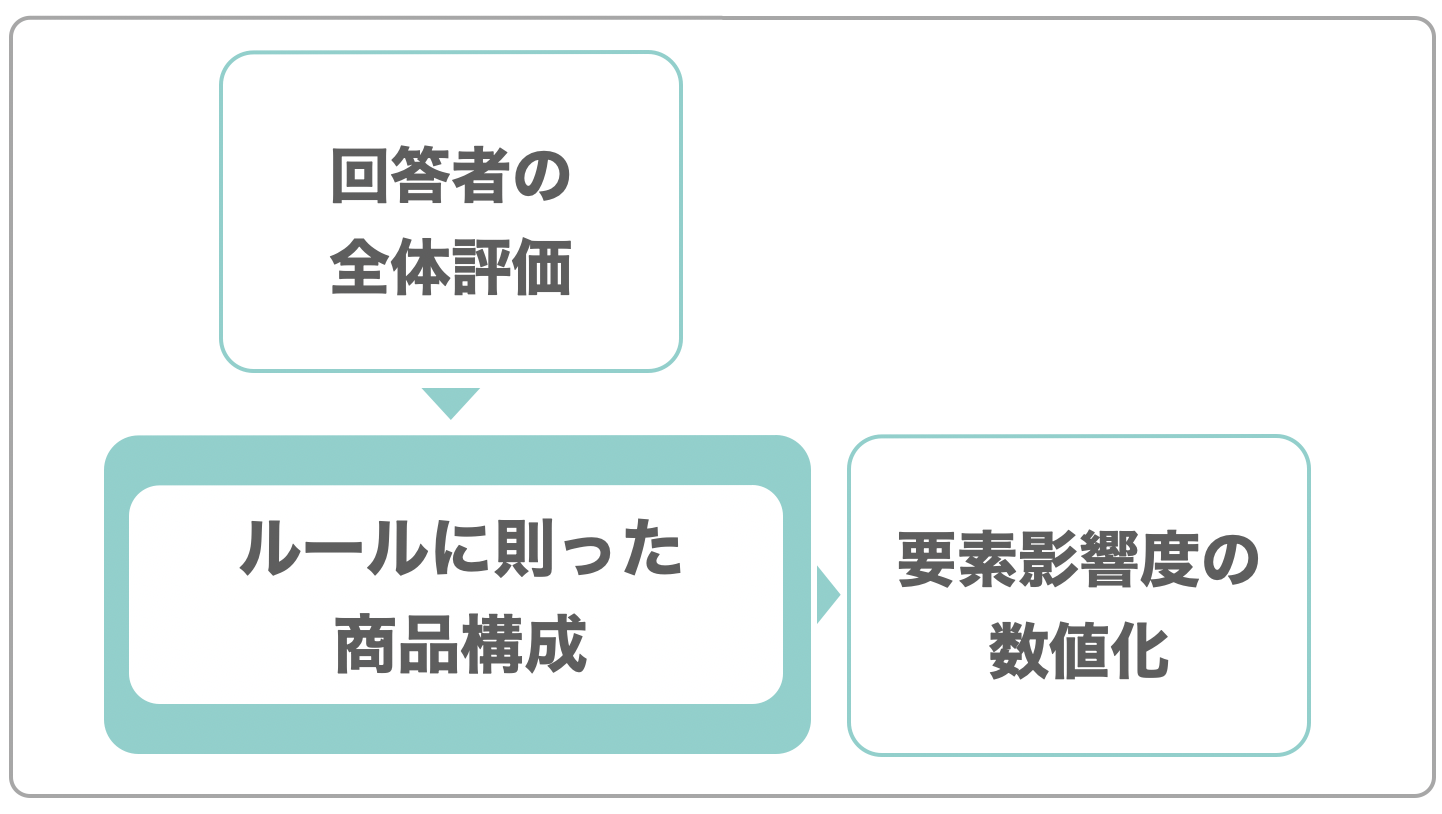
そのため「性能を引き上げる際の新価格」や、「新しい商品構成の検討」に活かすことができます。

つまり、コンジョイント分析には次のような特徴があります。

• 各要素の購買意欲を高める度合いを数値化することで、定量的に分析可能
• 少ない構成パターンの試行から、より良い商品構成を推測可能
• 全体評価だけを行うので回答者への負担が少なく、その分正確な回答が期待される

最終的に、購入者の意図や好みを分析することを目的として、新しい商品の構築をしていけるのがコンジョイント分析の強みでしょう。

コンジョイント分析の手順

コンジョイント分析では以下の言葉が使用されますので、ここで次の3つの用語を定義します。

• 属性＝商品の要素
• 水準＝商品の要素の具体的な数値や内容
• 効用値＝購買意欲を高める度合い

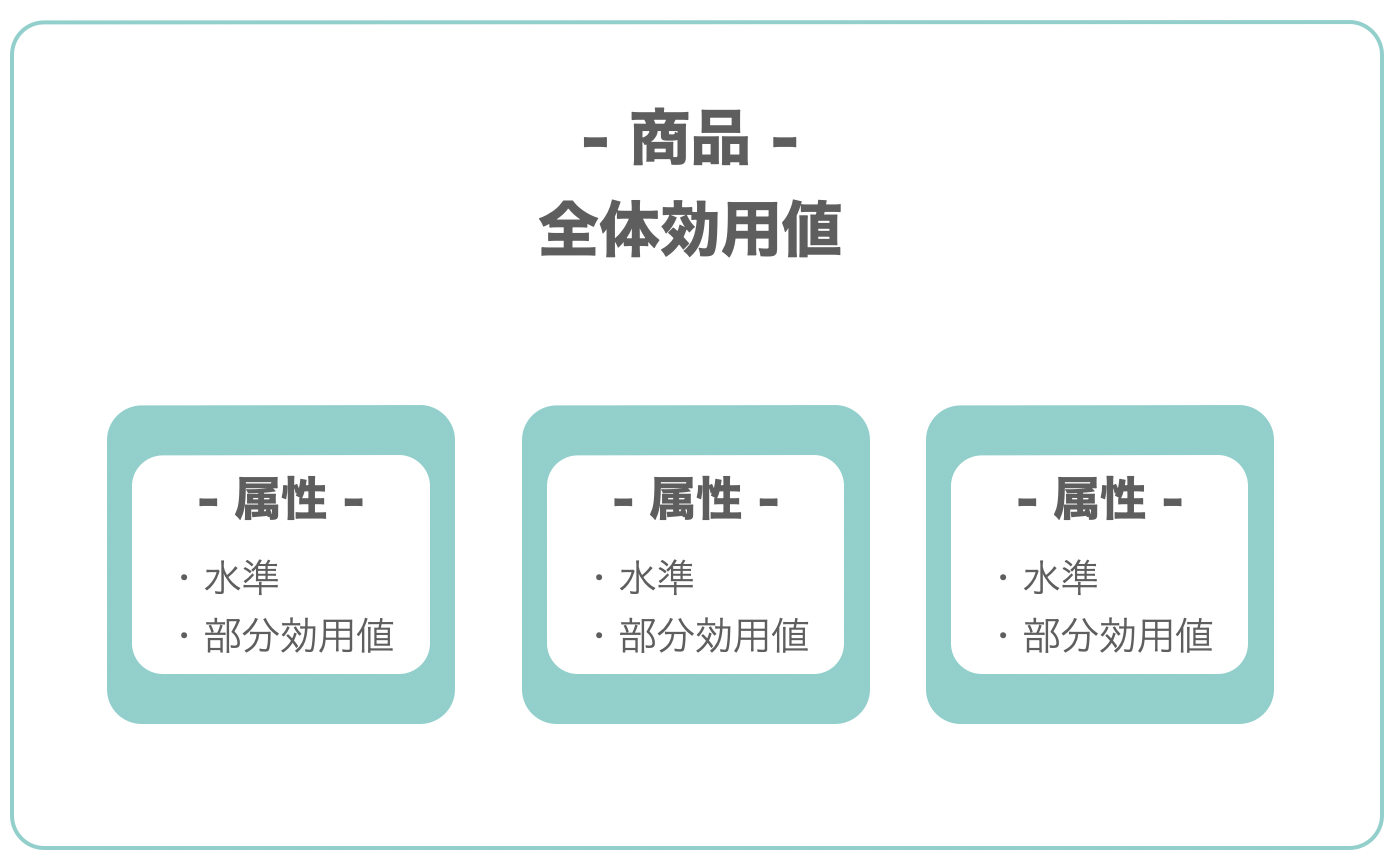
ここでも自動車を開発する際の例を使用して、分析の手順を順を追って説明します。

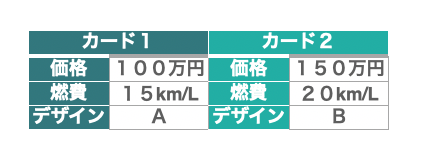
コンジョイント分析では、図4のようなコンジョイントカード（商品の各要素が書かれた表）を作る必要があります。 コンジョイントカードを作るためには、まず直交表を理解しておく必要があるので、そちらの説明から始めていきたいと思います。

手順１：直交表の理解

コンジョイントカードは、直交表の法則に従って作成する必要があります。 直交表とは、いずれの2列を取った場合でも、全ての水準の組み合わせが同じ数になっている配列表です。 直交表にはいくつも種類がありますが、今回は次の図5の直交表を使用します。

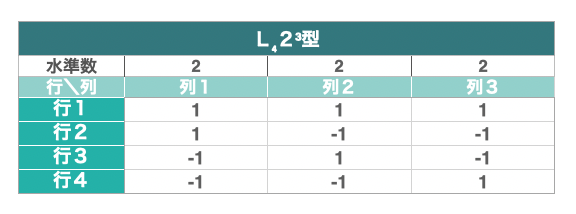
列を属性、行をカード、表の値を水準、というように当てはめていきます。

なぜ、この直交表に沿った組み合わせにすることで、少ないカードで部分効用値の測定ができるのかというと、ある水準に対して、その他の水準が偏りなく現れるようになっているからです。

例えば、列1の1という水準に対し、行1・行2の2枚のカードによって列2・列3では1と-1が２度ずつ現れています。 列1の-1という水準に対しても、行3・行4の2枚のカードによって列2・列3で1と-1が2度ずつ現れています。 同様に、列2や列3のいずれの水準を中心に見てみても、各水準が2度ずつ現れ、偏りがないようになっているのが分かります。

このように直交表は、偏りなく試行することによって少ないカード枚数での部分効用値の測定を可能にするのです。列2や列3のいずれの水準を中心に見てみても、各水準が2度ずつ現れ、偏りがないようになっているのが分かります。

手順２：コンジョイントカードを作る

では、図4のようなコンジョイントカードを作っていきましょう。 自動車の購入者が比較するであろう属性を挙げていきます。 今回は例として図５の直交表に合わせ、価格・燃費・デザインの3つの属性を考えることとします。

次に、水準を設定していきます。 水準では具体的に価格をいくらにするか、ということを決めていきます。 ここでは図5の直交表を参考に、水準数はすべて2つなので、価格は100万円を1の値に、150万円を-1の値に。燃費は20km/Lを1の値に、15km/Lを-1の値に。デザインはＡを1の値に、Ｂを-1の値にそれぞれ設定しました。 ここまでが次の図6になります。

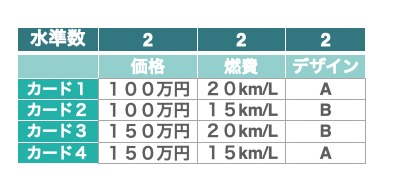
直交表の行の数がカードの数となりますが、見ての通り、全ての組み合わせを必要としません。 例えば、価格100万円で燃費20km/L、デザインＢという構成のカードなどは必要なく、今回の場合は4枚のカードを用意すればよいことになります。

み合わせの数に関して、今回の属性の組み合わせは「2³＝8」通りで、2が水準数、指数の3が属性数です。 属性数が増えると膨大な組み合わせになっていきますが、直交表を用いることで少ない試行回数になることが分かります。

手順３：実際に回答者に評価してもらう

次に、コンジョイントカードの評価方法を考えます。
先に述べたように、回答者には個別の要素ではなく全体評価のみを行ってもらいます。 よく使用される評価方法には、順位評価、得点評価、一対比較評価があり、またそれぞれの評価方法をとった場合の計算法は次の通りです。

なお、カードの数が増えると順位評価や、一対比較評価のような回答者に比較を求めるものは回答が難しくなります。

今回は得点評価を行うこととし、図7のようにランダムで評価を行いました。

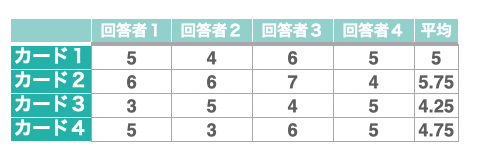
手順４：コンジョイント分析の計算

計算を行う段階では、数量化1類という解析を用います。

実際の計算には、エクセルやその他の分析ツールを用い、回帰分析を実行することにより行います。
回帰分析を行うにあたり、図5の直交表の「1と-1」の値を「1と0」の値へと変換し、さらに、先ほど回答した得点評価の各カードの平均得点を求め、表に付け足します。

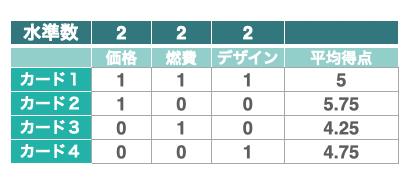
この図8が解析を行う最終的な状態となります。 また、価格・燃費・デザインのデータを説明変数、平均得点のデータを目的変数といいます。

図8のデータを使ってエクセルの回帰分析を実行すると、次のような結果が表示されます。

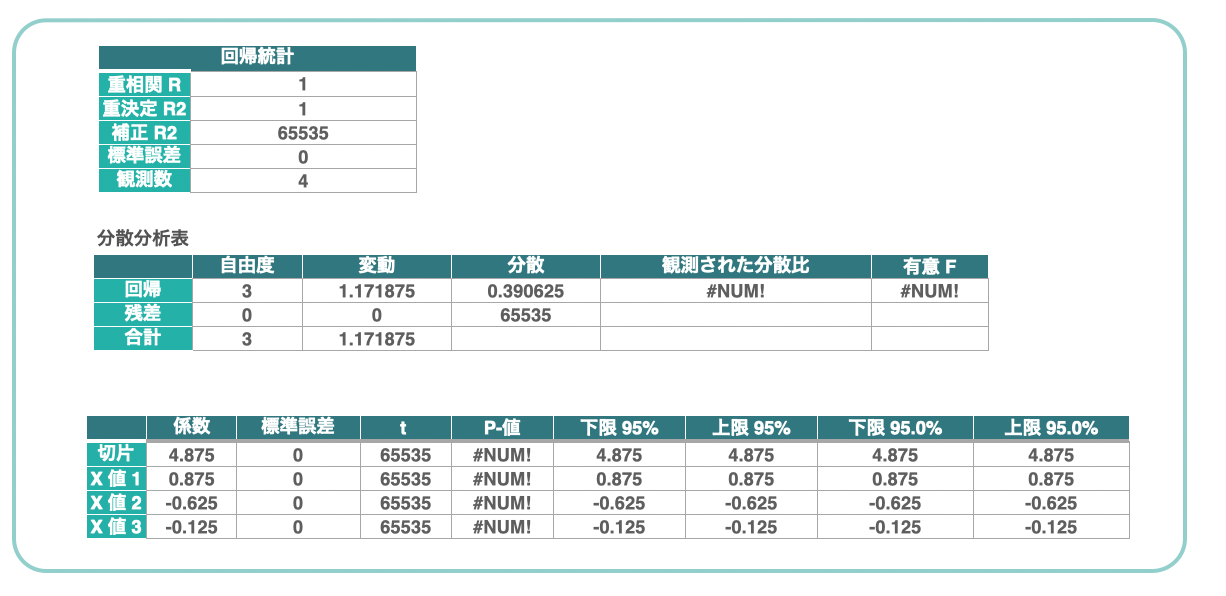
図9の左下、係数の値を回帰係数といい、部分効用値の算出に使用します。

部分効用値を導くには、まず加重平均を計算します。
加重平均は、「（0.4375×2＋0×2）÷4＝加重平均」のように求められます。
これを計算し、部分効用値を求めたものが次の図10になります。

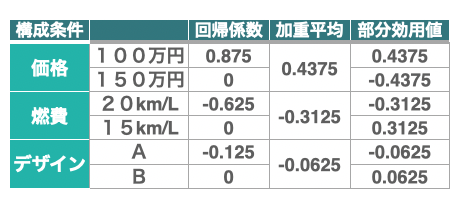
手順５：結果の分析

（ランダムに評価した）データの結果を見ていきます。

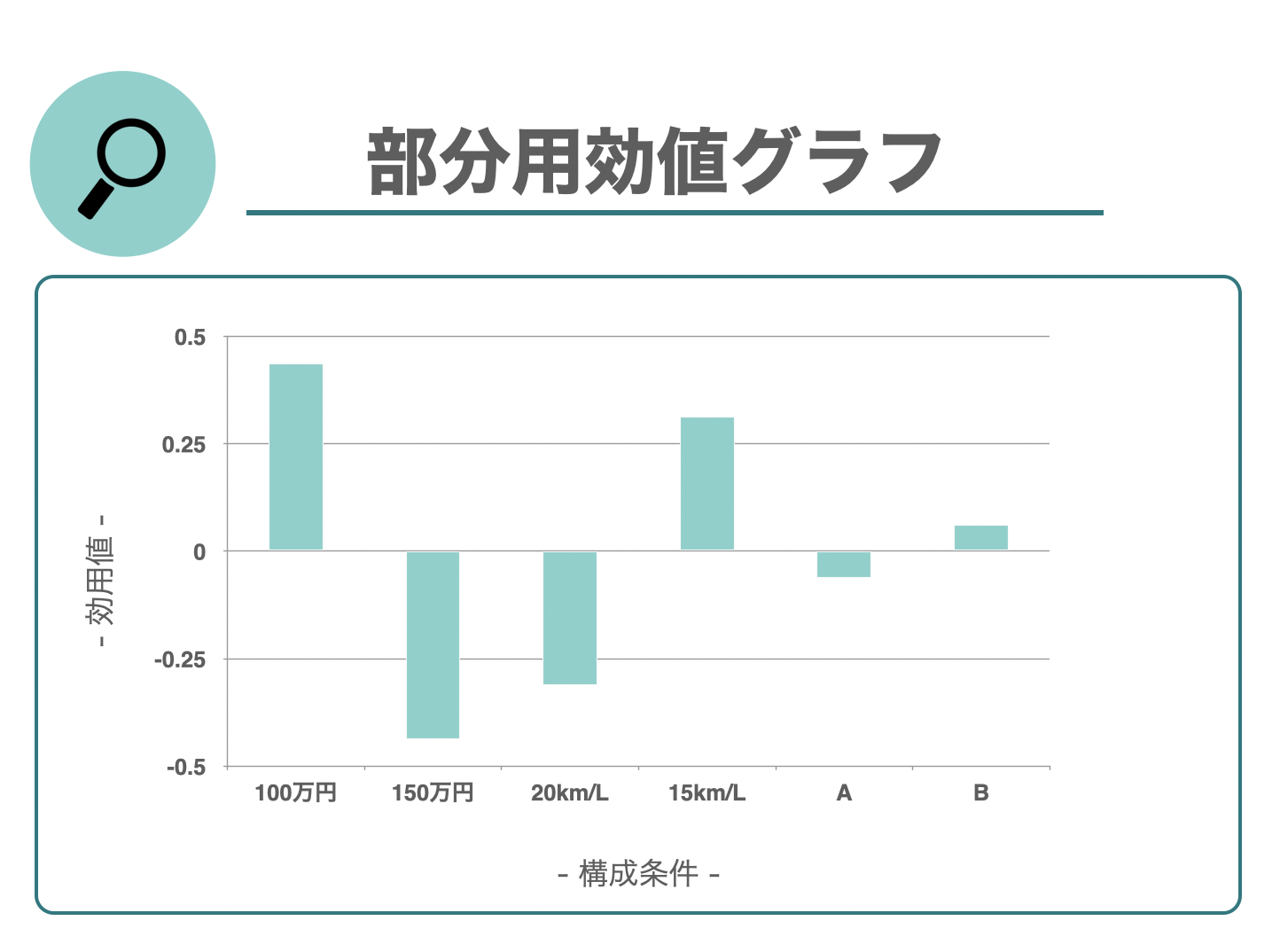
図10、及び図11の部分効用値グラフを分析していくと、価格100万円という要素が部分効用値0.43と最も大きな値になっています。 逆に、価格150万円のときには大きく効用値を下げています。 ここから今回、価格が全体効用値を決定する上で最も重要な要因になったと言うことができます。

次に、燃費に関しては燃費20km/Lの部分効用値ー0.31で、15km/Lのときは0.31になっており、「燃費が良くなると効用値が下がる」というおかしな結果になっていますが、評価はランダムに行いましたので、正しい結果が出ています

一方、デザインはAが-0.06で、Ｂが0.06と全体効用値への影響は小さく、購入者にとって重要な要因になっていないと読み取ることができます。 もしかしたら似たようなデザインになっているなど、車のデザインに魅力を感じられていない可能性がある、というような分析もできるかもしれません。

今回の分析で最も全体効用値が高い組み合わせは、100万円で15km/L、デザインＢになり、カードＢの商品構成ということになりました。 今回は評価を行ったものの中に全体効用値が最も高くなるカードがありましたが、評価を行っていないカードになることもあります。 このことは、コンジョイント分析を行うメリットでもあるのです。

また、評価を行っていないカードの評価（全体効用値）を推測したい時は、そのカードの属性がもつ部分効用値の合計と、評価を行った全てのカードの平均点を足した値で求めることができます。

コンジョイント分析の注意点

最後に、コンジョイント分析を使用する際の注意点は、水準の設定を適切に行わなければならないということです。
例えば図6において、自動車の価格を10万円と非常に安く設定すると、多くの人が選ぶ（高い点数をつける）ので部分効用値が高くなりすぎます。 そのことによりその他の属性が軽視され、不正確な結果になるでしょう。

このように注意すべきこともありますが、コンジョイント分析は、「商品スペックを高くした時いくらで売れるか」といったことや、「少ない試行からより良い商品コンセプトをみつける」など、ビジネスに幅広く応用できる手法ということができます。