相関分析とは?相関分析の基礎を解説、実際の分析方法も紹介!
2022年09月09日
データを扱う中で、それらのデータの関係性から説得力のある主張を考える時にも活用できます。本記事では相関分析について、その概要や実施の流れ、どのようにしたら有効活用できるのか、を見ていきます。
相関分析とは?
一度は「相関分析」という言葉を聞いたことがある方も多いと思います。
相関分析のやり方について触れる前に、相関分析の基本について解説していきます。
相関分析とは?
まず相関分析の定義を確認してみましょう。
相関分析とは、2つの要素間の関係性を理解する手法のことです。
2つの要素が「どの程度同じような動きをするか」を明らかにし、データの特徴を簡単に把握できるという特徴があります。
相関関係と相関係数
まず相関分析を理解するには相関関係がどういったものなのか、を知る必要があります。
- 相関関係
- 一方の変数が増加すると、もう一方が増加または減少するような、二つの数値の関係のこと。
例えば、ある15人のクラスで数学と理科、国語のテストを行い以下のような結果が得られたとします。
| 出席番号 | 数学(点) | 理科(点) | 国語(点) |
|---|---|---|---|
| 1 | 90 | 90 | 66 |
| 2 | 75 | 75 | 77 |
| 3 | 70 | 70 | 51 |
| 4 | 69 | 69 | 66 |
| 5 | 85 | 85 | 71 |
| 6 | 95 | 95 | 74 |
| 7 | 69 | 83 | 80 |
| 8 | 90 | 90 | 90 |
| 9 | 75 | 75 | 88 |
| 10 | 70 | 70 | 51 |
| 11 | 90 | 90 | 68 |
| 12 | 80 | 80 | 56 |
| 13 | 60 | 60 | 79 |
| 14 | 81 | 81 | 66 |
| 15 | 55 | 55 | 77 |
この時、「理科と数学」「国語と数学」の点数で比較し、相関関係を明らかにしようとすると、以下のように表すことができます。
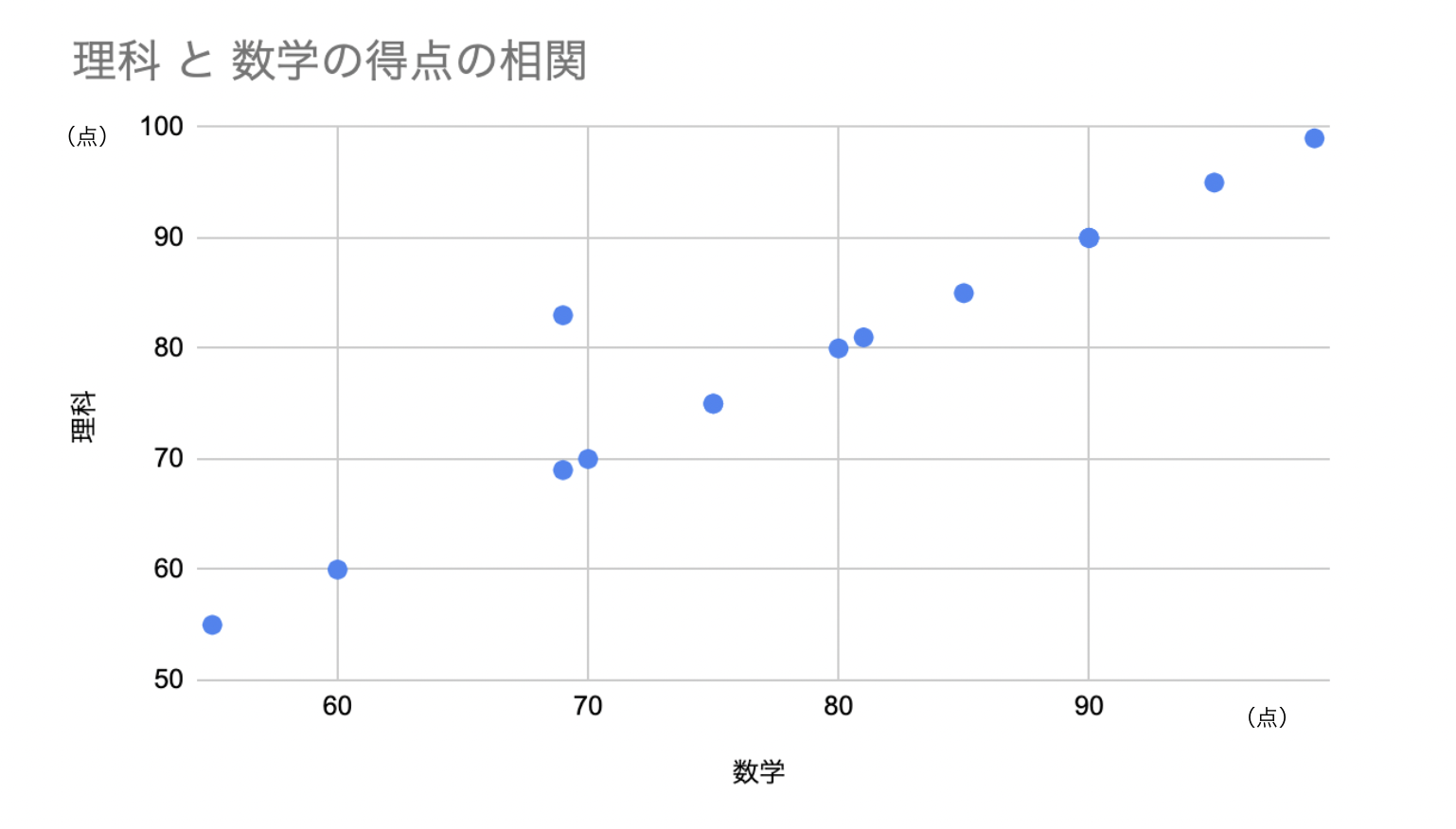
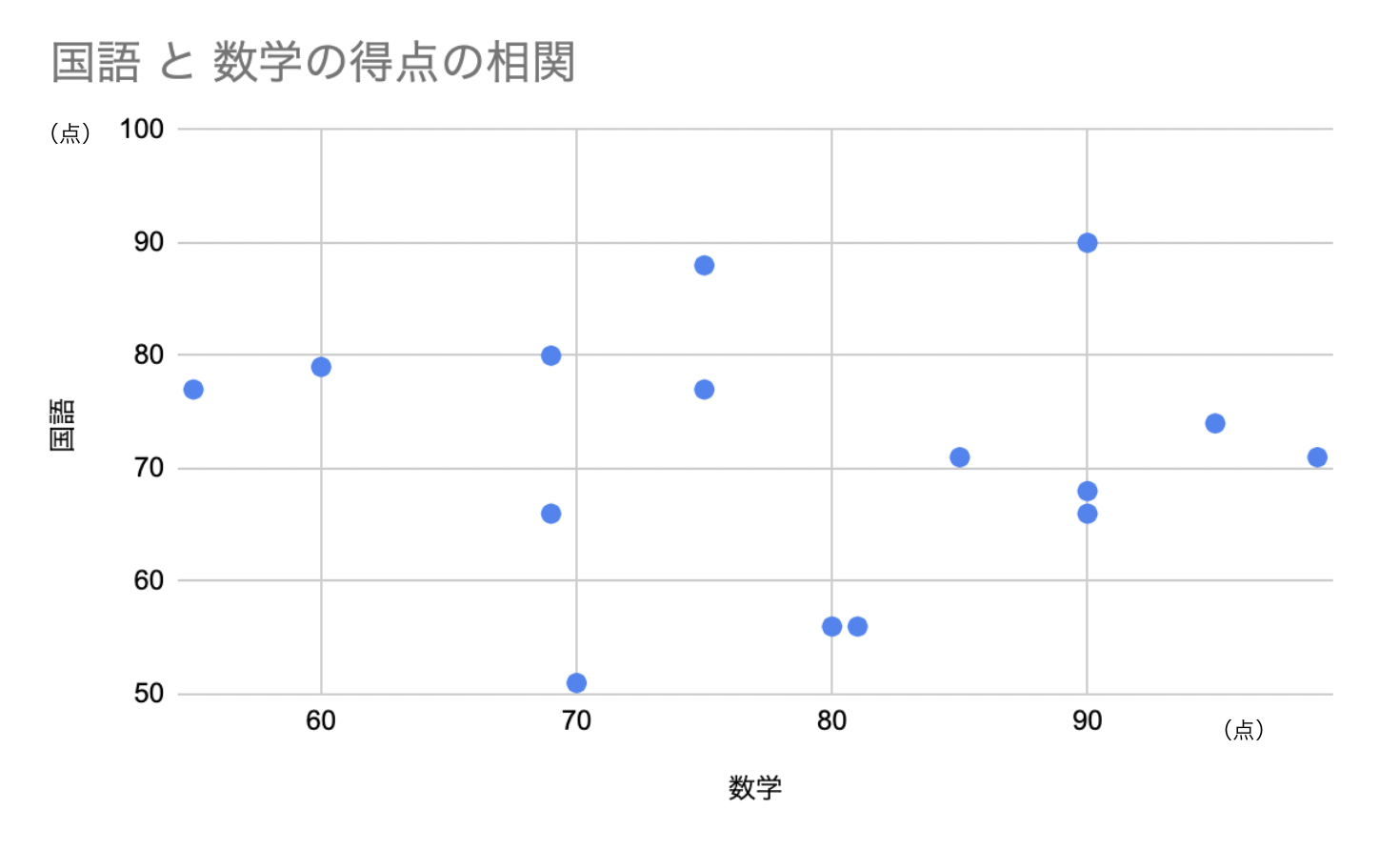
理科と数学のテスト得点を比較したグラフは、理科の得点が高い人ほど数学の得点が高い場合が多く、相関関係があると言えます。
それに対して、国語と数学のテスト得点は国語の得点が高いからといって数学の得点が高くなったり低くなったりといった変化がなく、相関関係がないと分かります。
次に「相関関係」と言う言葉とセットで使われることが多い相関係数とは何なのか、見ていきましょう。
- 相関係数
- 2種類のデータ間の関連性の強さを示す指標。-1から+1の間の値で表す。
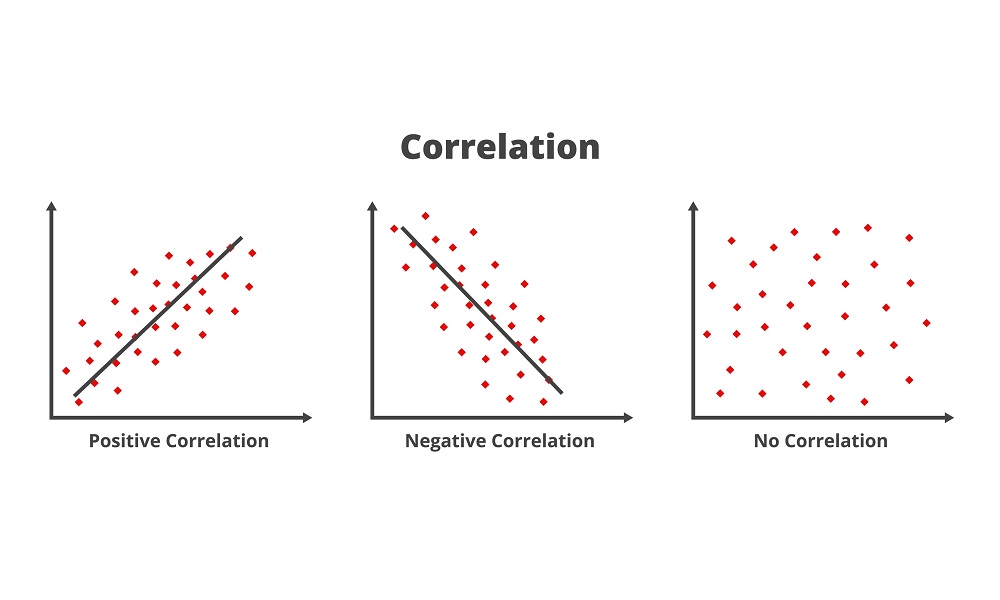
2種類のデータ間の関連性には以下の3種類があります。
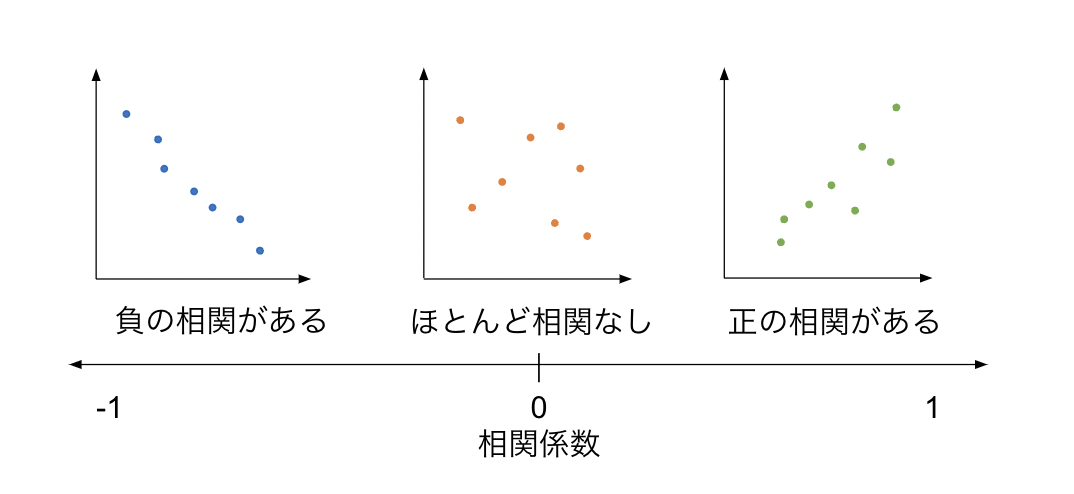
- 正の相関
「片方の数値が変化するとき、もう片方の値も同様に変化する」関係性。相関係数は正の値になる。 - 負の相関
「片方の数値が変化するとき、もう片方の値は反対に変化する」関係性。相関係数は負の値になる。 - 無相関
「片方の数値が変化するとしても、もう片方の値に決まった変化が見られない」関係性。相関係数は0になる。
このように相関関係には大きく分けて3つの関係性があり、こうした関係性からデータの特徴を捉えることができます。
回帰分析との違い
データ分析の方法は多くありますが、分かりやすいと言われ、よく取り上げられる分析方法は今回解説する「相関分析」と「回帰分析」の2つがあります。
その2つの相違点を見ていきましょう。
- 相関分析
- 2つ以上の変数の中から2つの変数に着目してそれらのもつ相関関係を求める手法
- 回帰分析
- 相関関係や因果関係があると予測される変数について、結果に値する目的変数に対し、要因となる説明変数を用いた予測式(回帰直線)を求める手法
*説明変数が1つなら単回帰分析、2つ以上なら重回帰分析と言います
相関分析も回帰分析も散布図を確認したり、基本的に2つの変数の関係性を形にしたりする点では共通しています。
しかし、相関分析と回帰分析は明らかに行う目的が異なります。
回帰分析は1つの変数から別の変数を予測する分析方法で、y=ax+bのような回帰式を求めることで、xからyを予測する、というように変数の予測をすることが目的です。
回帰分析は2つの数に因果関係を見出して考えますが、相関分析においては2つの変数に相関関係はあっても因果関係はないという点に特徴があります。よって、相関分析を行ってもy=ax+bというような式は出てきません。
相関分析の流れ
ここまでで相関分析がどういったものなのか、説明してきました。次に相関分析のやり方を順に追っていきましょう。
相関分析は散布図の作成、近似曲線の作成、相関係数の算出、そして検証の4つのステップで行われます。1つ1つのステップで具体的にどのようなことをするのか、詳しく見ていきましょう。
散布図の作成
散布図は縦軸と横軸にそれぞれ変数を設定し、個々の数値をXY平面上に配置した図のことです。散布図を用いることで、データがどのようにばらついているか、相関関係があるのか、を目視で確認できるようになります。
散布図の描画は相関分析の基本です。散布図を確認しないと誤った分析に繋がることが多々あるので、相関分析を行う際は必ず散布図を作成することをおすすめします。
近似曲線の作成
散布図を作成するだけでは傾向が分かりづらいこともあります。その場合に役立つのが近似曲線の作成です。
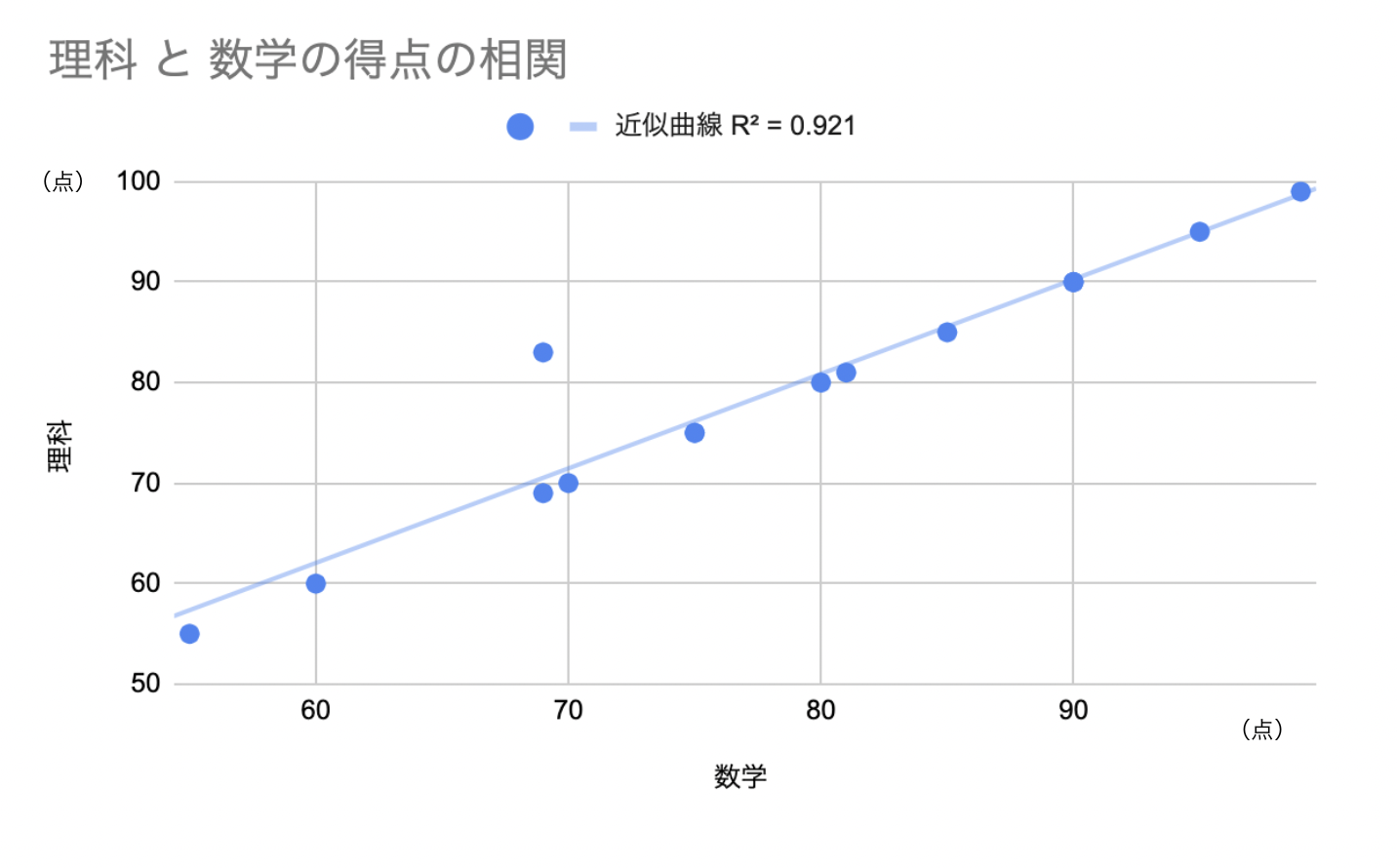
近似曲線は各データを数学的に処理することで「妥当と思われるライン」を上記のように描画したものです。実際のデータは、作成した近似曲線とずれますが、このずれが最大限小さくなるように近似曲線がひかれているのです(上のグラフでは、凡例に「R2=0.921」とありますが、これは「実際にどのくらい直線に近いのか」を示す数字です。これが1だと実際のデータが完全に近似直線の上にのる状態を表します)。
「近似曲線」を書くことで、データの傾向を把握しやすくするため、大まかなイメージではなく数式として捉えられるようになります。
また、適切な近似曲線を選択している場合には、近似曲線は前後に延長することで「データがない部分」の予測をするときにも活用できます。
相関係数を算出
次に相関係数を求める必要があります。実際に求める式、手順を見ていきましょう。
xとyの相関係数 =(xとyの共分散)÷(xの標準偏差)÷(yの標準偏差)
- ◆相関係数の求め方
- それぞれの変数の平均値を求める
それぞれの変数の偏差(数値ー平均値)を求める
それぞれの分散(偏差の二乗平均)を求める
それぞれの変数の標準偏差(分散の正の平方根)を求める
共分散(偏差の積の平均)を求める
共分散を2つの変数の標準偏差で割って相関係数を得る
このような流れで相関係数の数値を求めることができます。
相関係数の検証
相関係数を算出したところでどのような分析、考察を考えることができるのでしょうか。
相関係数は-1から1の間で割り出され、1に近い値が出た時は正の相関が強く、-1に近い時は負の相関が強いと考えられます。
相関分析を生かすには?
相関分析で気をつけること
ここまで相関分析とは何なのか、相関分析のやり方を見てきました。相関分析の実際のイメージが湧いたところで、相関分析で気をつけることを見ていきましょう。
まず、心がけるべきなのは「見かけの相関に気をつける」ことです。
相関分析の結果から因果関係を推測することは、誤った因果を想定する危険性があるので注意が必要です。
回帰分析との比較でも述べたように相関分析から因果はわかりません。そのため相関分析の結果はあくまで「仮説」と捉え、そこに因果関係を見出す際には「検証」が必要であることを念頭に置くことがおすすめです。
次に相関分析の結果の数値だけでは、「一直線以外の関係性は捉えられない」という特徴があります。一直線以外の何かしらの法則性については、相関分析をする際に散布図を描画することで見落としを防ぐことが可能になります。
そして、相関分析の結果は外れ値に影響されやすいということを頭に置いておく必要があります。
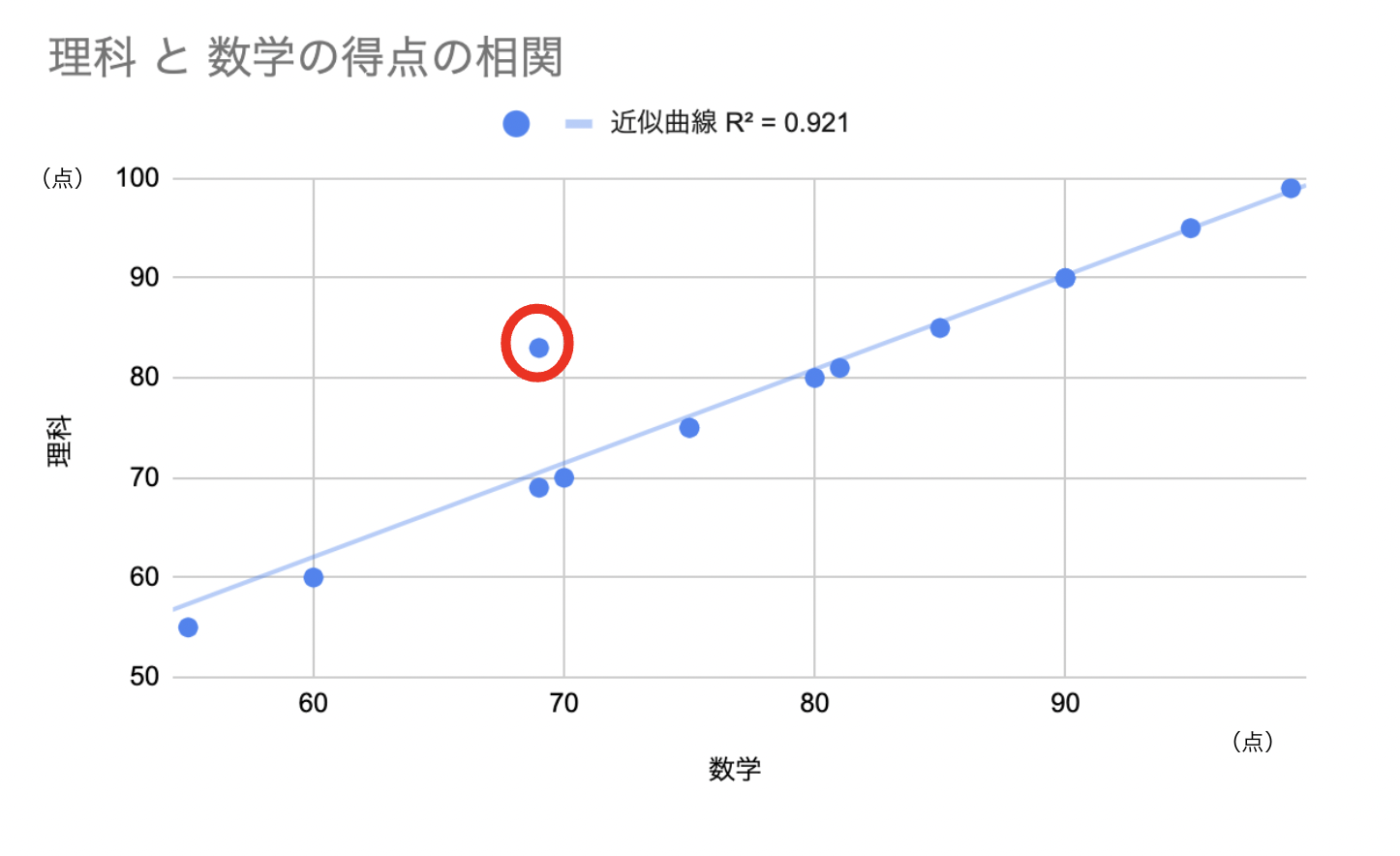
外れ値は上の図で赤で囲まれている値のように、得られた値のうち推定値との差が異常に大きい値のことです。
相関分析は平均値からの差を用いて分析する手法であるため、異常に大きかったり小さかったりする外れ値に大きな影響を受けます。
そのため、外れ値に考慮して分析を進める必要がありますが、外れ値に注目して分析を行うことで新たな発見を得ることもできます。
相関分析が有効な場面
ここまでで「見かけの相関に気をつける」「一直線以外の関係性は捉えられない」「相関分析の結果は外れ値に影響されやすい」ことに気をつけると良いということが分かりました。
こうしたことに気をつけた上で相関分析の有効性を特に生かせるのはどのような時なのでしょうか。
まず、大量のデータから関係性のある項目を抽出したいときが挙げられます。相関分析は、2つのデータに関係性があるか明らかにする、シンプルな分析方法であるため、大量のデータの中からでも簡単に関係性を見出すことができます。
そして、関係性があることを客観的に示したいときにも使うことができます。項目が多くなればなるほど、人間の目でそれぞれの関係性を見つけるのが難しくなります。相関分析で各項目の関連性を数値にすることで、客観的な判断材料として提示することができます。
まとめ
本記事では相関分析について、その概要や実施の流れ、どのようにしたら有効活用できるのかを紹介しました。
相関分析は手軽に行えてインパクトのある発見や説得材料を与えてくれるので非常に便利な手法です。
しかし、同様に、相関係数が1あるいは-1に近い値を示したからといって、必ずしも2つの変量に関係性があるともいい切れません。全く関係性のない変数を並べても、偶然にも関係性があるかのような相関係数が出てしまうことがあります。
相関分析を行う場合は、散布図を作成して、2つの変量の散らばりを目で確認するとともに、数値などの裏に隠された背景がどのようなものなのかを注意深く分析していくと良いでしょう。
- サービス概要を無料配布中「3分で読めるGMOリサーチのサービス」
-
GMOリサーチはお客様のマーケティング活動を支援しており、さまざまなサービスを提供しております。
- スピーディーにアンケートデータを収集するには
- お客様ご自身で好きな時にアンケートを実施する方法
- どこの誰にどれくらいリーチができるか
ぜひこの機会にお求めください。 - 資料請求する


