【図解】平均値・中央値・最頻値の意味と使い分け
2022年12月09日
平均値は「データを単純に足し、その合計値をデータの数で割ったもの」です。平均値と同じく、データ分布の特徴を表す指標には、中央値や最頻値があります。
この記事では、平均値・中央値・最頻値との違いと使い分けの方法を解説します。
平均値の定義と算出方法
データの平均を算出する方法には複数の種類があります。例えば、算術平均・加重平均・幾何平均・調査平均などです。
この記事では、最もポピュラーな指標である単純算術平均を取り上げ、以下のように定義します。
平均値(Mean)※単純算術平均
データを単純に足し、その合計値をデータの数で割ったもの。
例えば、プロスポーツチームが、以下の3試合における観客動員数平均値を求めたい場合を考えてみましょう。3つの試合でそれぞれ、27,000人、25,000人、26,000人の観客を動員したとします。このとき平均値は以下から、26,000人と計算できます。
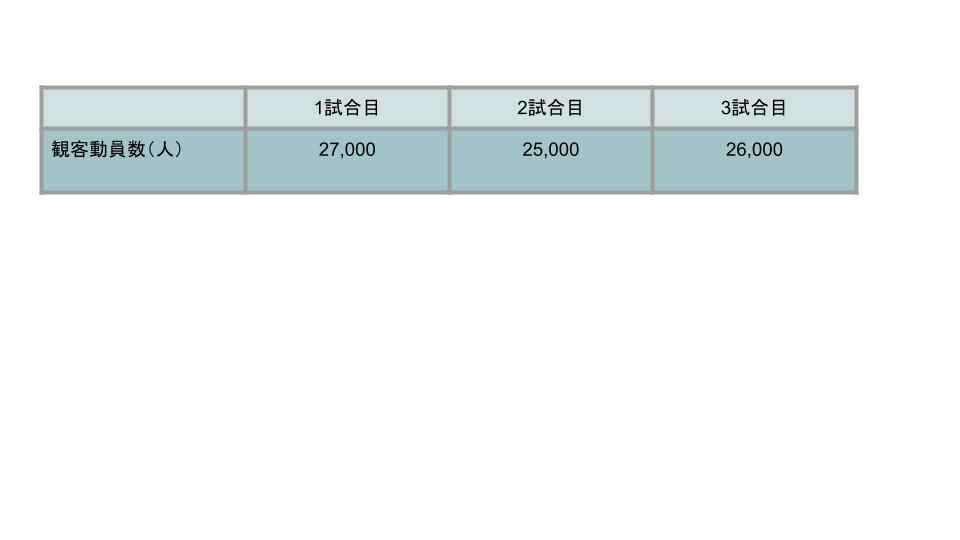
観客動員数平均値=(27,000+25,000+26,000)÷3=26,000人
平均値を求めることで、データが膨大であっても、データ全体の特徴を端的に知ることができます。
平均値のようにデータの特徴を表す指標のことを「要約統計量」「代表値」と呼びます。
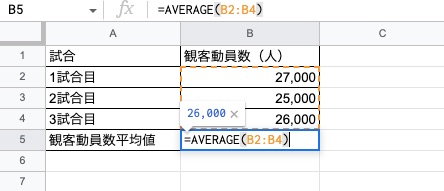
なお、Excel・Googleスプレッドシートなどの表計算ソフトでは、AVERAGE関数を用いることで平均値を算出可能です。
平均値=AVERAGE(範囲)
平均値と中央値・最頻値の比較
要約統計量(代表値)は、平均値以外にも存在します。
平均値以外の要約統計量として、中央値と最頻値を解説します。
中央値
中央値(Median、 メジアン、メディアン)は、「データを昇順または降順並べたときに、ちょうど真ん中にあたる値」です。
例えば、あるプロジェクトにおける5年間の費用を比較したいケースを考えてみましょう。
概ね100万円前後で推移していたプロジェクトでは、ある年だけ機器の買い替えが発生し、300万円になってしまったとします。
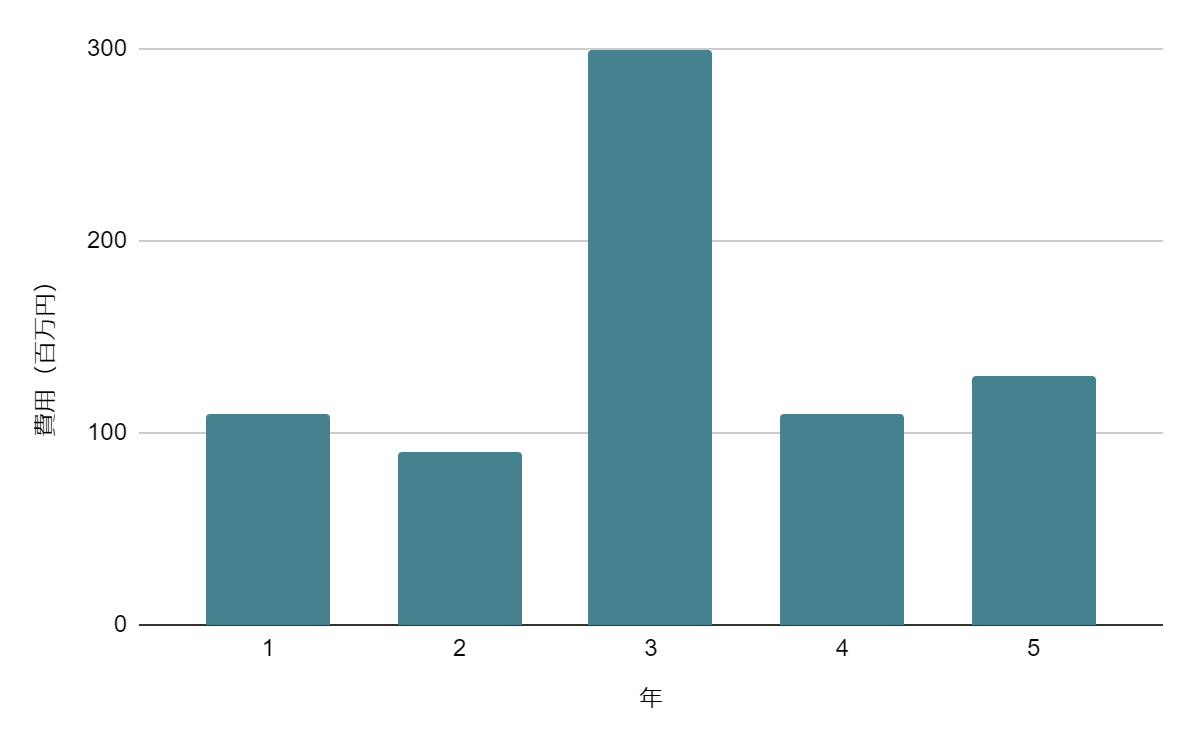
| 年 | 1年目 | 2年目 | 3年目 | 4年目 | 5年目 |
|---|---|---|---|---|---|
| プロジェクトの費用 | 110万円 | 90万円 | 300万円 | 110万円 | 130万円 |
このとき、平均値を見ると148万円となりますが、3年目の余分な出費がなければもう少し平均値は下がることが予想できます。
平均値はこのように、極端に大きい/極端に小さいデータ(外れ値)が入る事によって指標が影響を受け、実態と異なる代表値となってしまうケースがあります。この場合は、別の代表値である中央値を用いることで、外れ値の影響を受けにくくできます。
上記データの中央値を見るために、データをプロジェクト費用の昇順に並び替えます。
| 年 | 2年目 | 1年目 | 4年目 | 5年目 | 3年目 |
|---|---|---|---|---|---|
| プロジェクトの費用 | 90万円 | 110万円 | 110万円 | 130万円 | 300万円 |
中央値は、データを昇順または降順に並び替えたときに真ん中にある値となるので、今回の場合、4年目の「110万円」が中央値となります。
このようにデータの外れ値の影響を少なくすることで、より実態に近い指標を得ることができたのではないでしょうか。
ExcelやGoogleスプレッドシートなどの表計算ソフトでは、中央値はMEDIAN関数で算出できます。
中央値=MEDIAN(範囲)
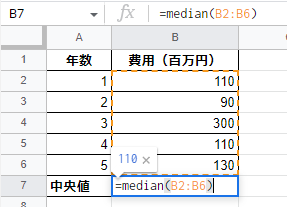
手動で計算する場合は、中央値はデータ数が偶数か奇数かによって計算方法が変わります。
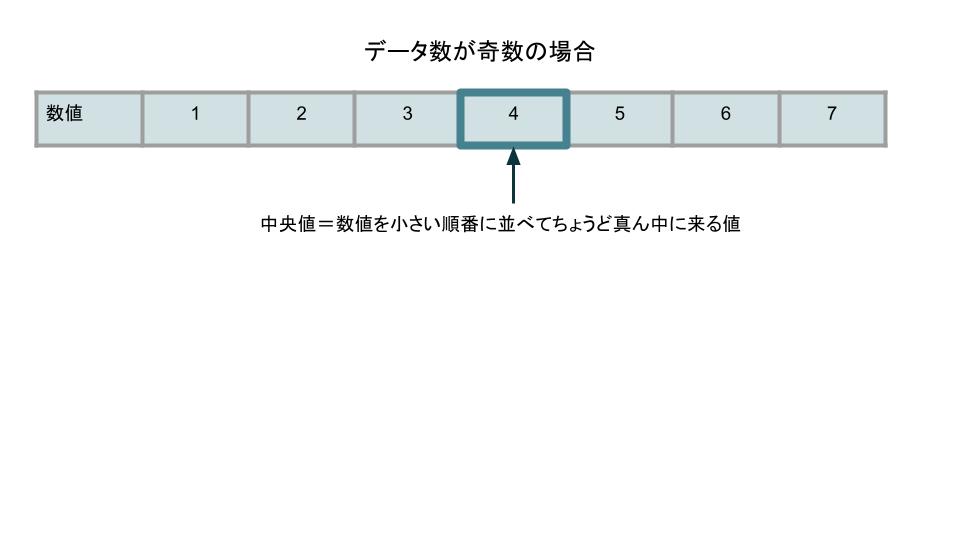
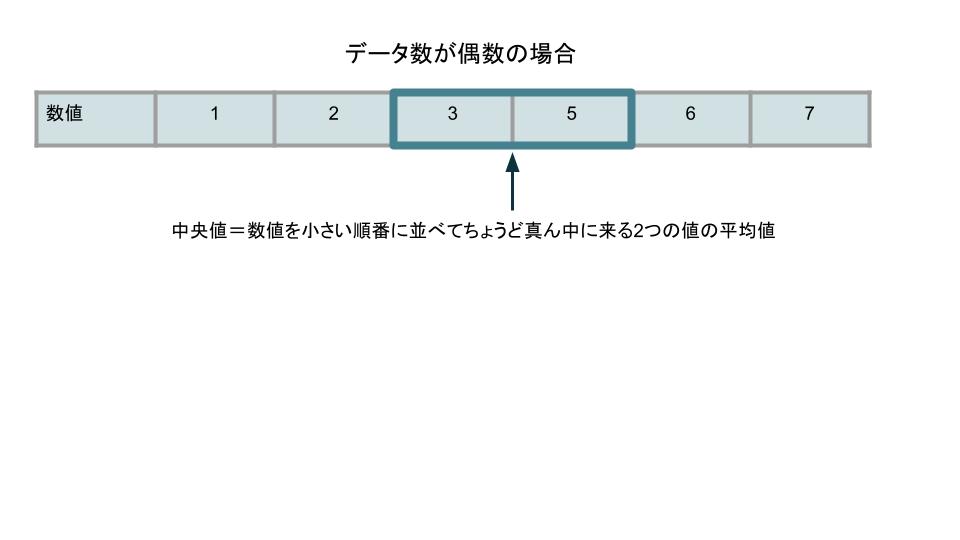
◆中央値の計算方法
| データ数が奇数の場合 | 数値を小さい順番に並べてちょうど真ん中にあたる値 |
|---|---|
| データ数が偶数の場合 | 数値を小さい順番に並べてちょうど真ん中にあたる2つの値の平均値 |
最頻値
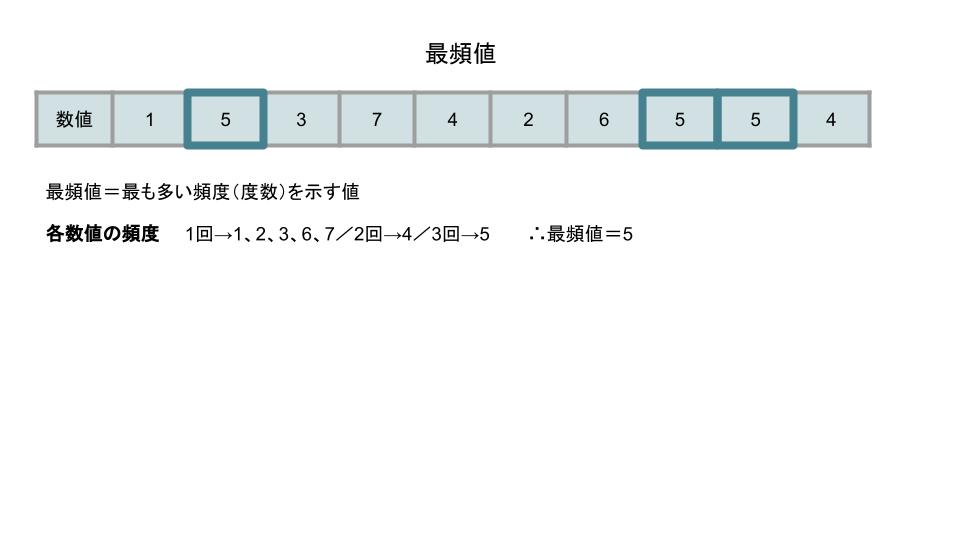
最頻値(Mode, モード)は、最も多い頻度(度数)を示す値です。
例えば、「1、5、3、7、4、2、6、5、5、4」という10個のデータがあるとしましょう。このとき、データの中で最も多く現れた値は「5」(3回)です。そのため、最頻値は「5」となります。
平均値・中央値ではなく最頻値が求められるシーンにはどのようなものがあるのでしょうか。
例えば、あるテストにおいて、9人の成績が「100点、200点、200点、200点、400点、700点、800点、800点、900点」だったとしましょう。
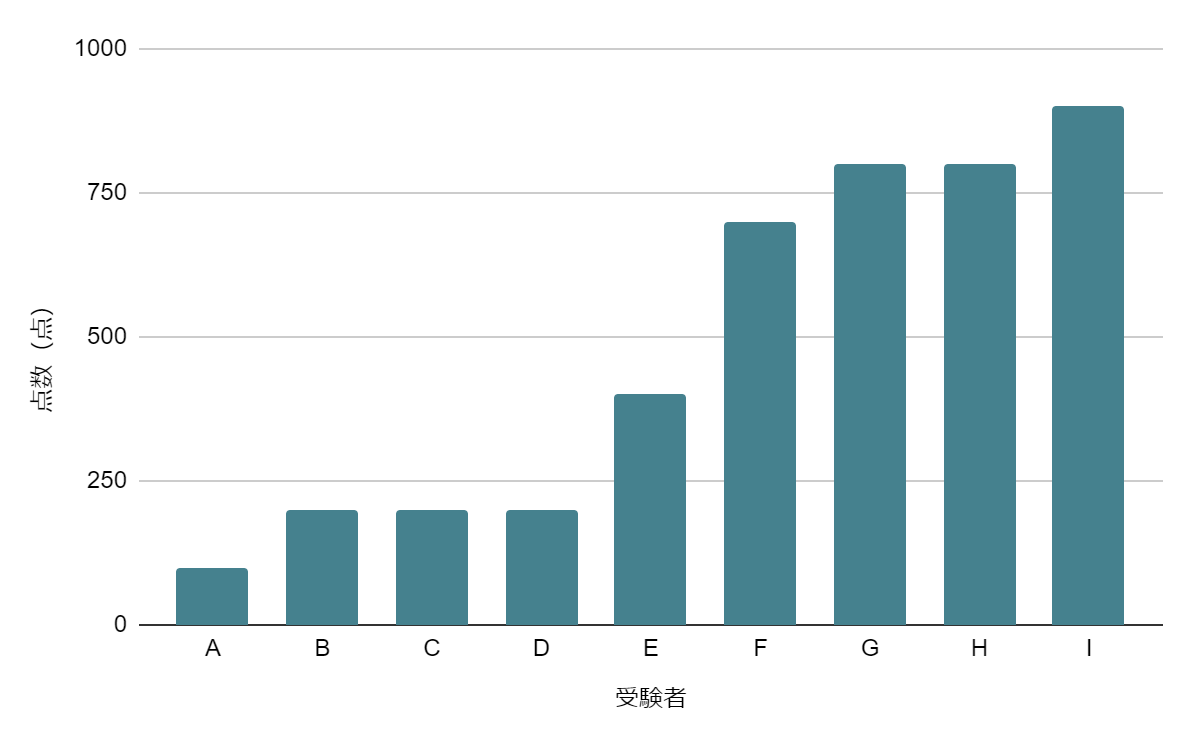
このとき平均値を見ると430点、中央値を見ると400点となります。しかし、平均値・中央値には大きな差はないものの、度数分布表を見ると最頻値はそれらよりも低い数値であり、分布に偏りがあるグラフとなっています。
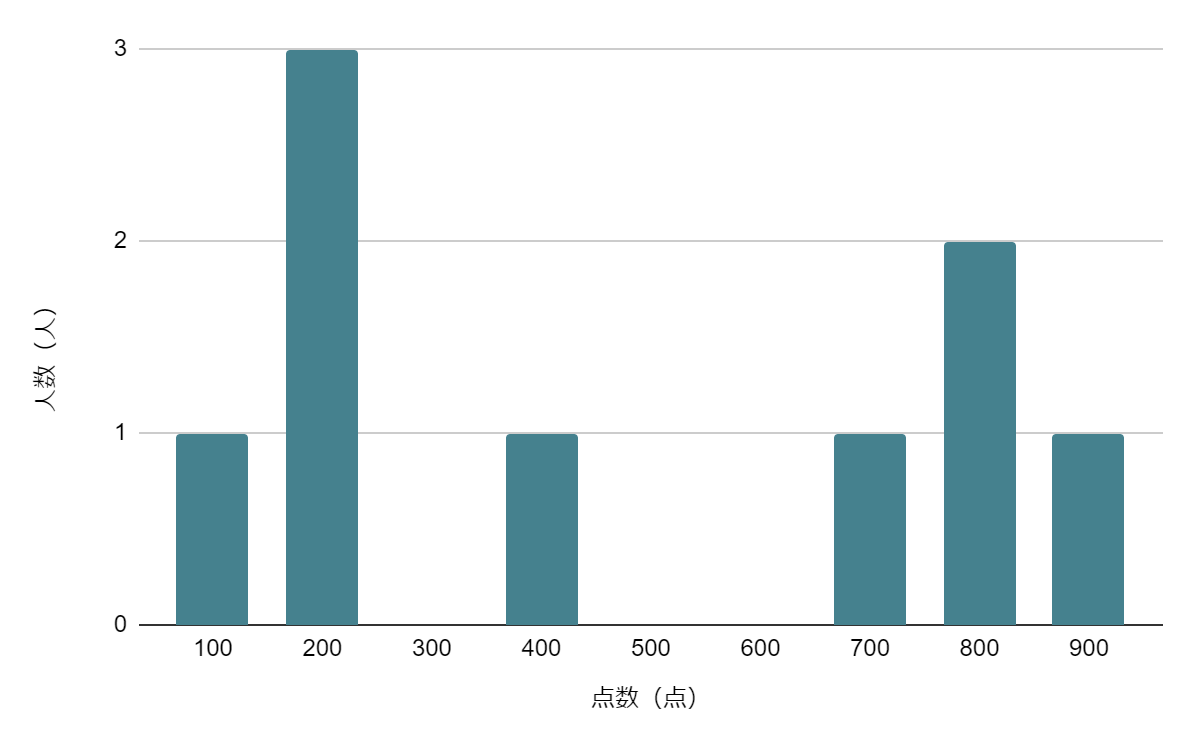
このように、最頻値を見ることで、データの特性をさらにわかりやすくできます。この例では、最も多い頻度(度数)を示す点数は「200点」なので、最頻値は200点となります。
最頻値はこのように、最も多く現れた数値を指標とするため、外れ値の影響を受けにくく、かつ中央値よりも分布をある程度配慮できる要約統計量です。
ただし、最頻値はデータ数が少ないケースでは有効に使えません。例えば「1、5、3、7」のようにそれぞれが一度ずつしか出ない場合、無理やり最頻値を導こうとすると「1、5、3、7」のすべてが最頻値となってしまい、データの特性が見えづらくなってしまいます。
平均値・中央値・最頻値の使い分け
データの特性を把握するための指標には、平均値だけでなく中央値や最頻値なども挙げられます。
データの外れ値やデータのばらつきなどに応じて、平均値以外の指標も合わせて見ることで膨大なデータの特徴をより正確に捉えやすくなるでしょう。
最後に、平均値・中央値・最頻値の使い分けをまとめておきましょう。
| 平均値 | データ全体やデータ間で比較を行いたい場合 |
|---|---|
| 中央値 | データに極端な外れ値がある場合 |
| 最頻値 | データに大きなばらつきがある場合 |
平均値はデータ全体を対象とするため、例えばビジネスにおいては以下のようなシーンで活用すると良いでしょう。
| 平均値を使うべきシーン | シーンの例 |
|---|---|
| データ全体の変化を比較したい | 例:前年度と今年度で、漁港Aにおけるサンマの漁獲量を比較 |
| データ間の比較を行いたい | 例:A工場とB工場とで、製品Cの作成に必要な平均コストを比較 |
まとめ
要約統計量を見ることで、データの特性を端的に把握できます。平均値は使い勝手がよく有名ですが、外れ値の影響を受けやすく、利用シーンによってはデータの特性を正しく表せないこともあります。
中央値や最頻値をシーンに合わせて活用し、データの特性を正しく簡単に把握しましょう。
- サービス概要を無料配布中「3分で読めるGMOリサーチ&AIのサービス」
-
GMOリサーチ&AIはお客様のマーケティング活動を支援しており、さまざまなサービスを提供しております。
- スピーディーにアンケートデータを収集するには
- お客様ご自身で好きな時にアンケートを実施する方法
- どこの誰にどれくらいリーチができるか
ぜひこの機会にお求めください。 - 資料請求する


