商品を販売する上で最も重要な要素について考えたことはあるでしょうか？ 商品のプロモーションを促進するためには、例えば以下の重要度を明確にする必要があります。

• ブランディング
• 魅力
• 価格
• 人気度
• デザイン
• オプション機能

では、顧客の購買決定要因に最も大きく関わるのはこの内の一体どれなのでしょうか？

この購買決定要因の重要度の分析に役立つのがパス解析です。 パス解析を活用することで、商品販売戦略・自社サービスの更なる改善・顧客の創出などにますますリサーチを役立てやすくなります。

パス解析とは

たとえば、人気のスマホについて、どういった要因によってそれが決定づけられているのか知りたいとしましょう。 そもそもスマホの購入を決定づける要因は、以下のような要因が複雑に絡み合っていることが想定されます

◆スマホ購入を決定づける要因（想定）

こういった多種多様な要因について「どの要因がどれだけ人気度に影響を及ぼしているのか」と考えるとき、パス解析が役立ちます。

パス解析では、リサーチの結果に単回帰分析や重回帰分析をおこない標準偏回帰係数・標準化係数を算出することから、要因それぞれの影響度を定量的に把握することが可能です。

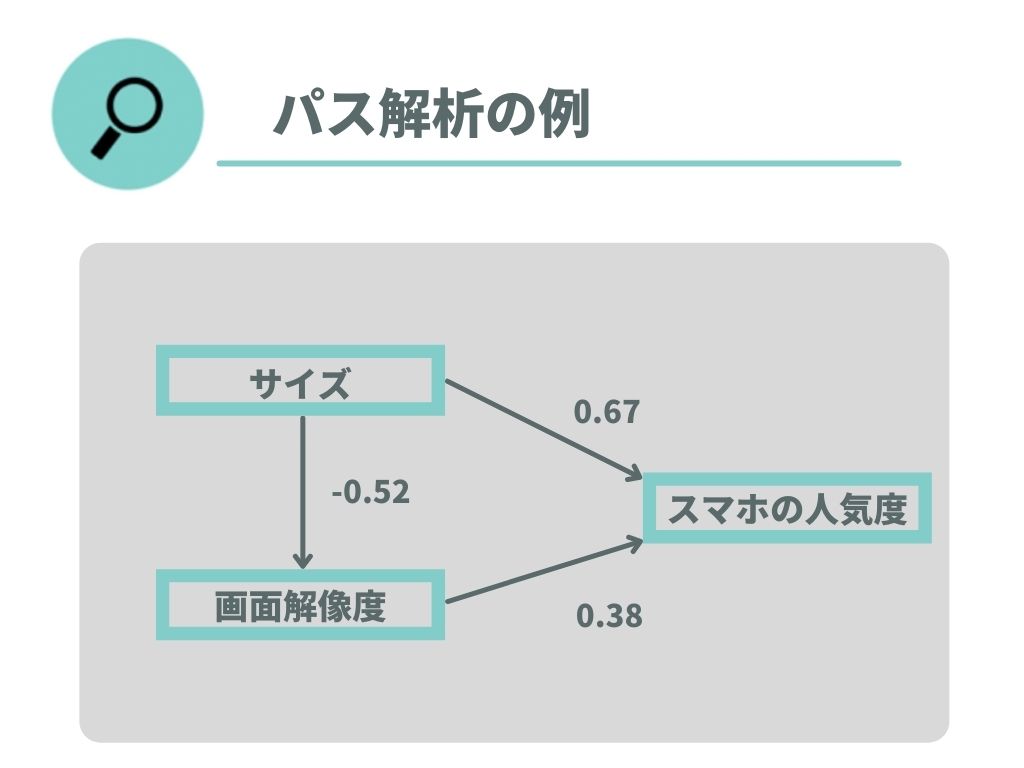
上の図からは、こういったことが分かります。

このようにパス解析は、要因自体が相関していて、それがある目的となる変数（今回で言えば、人気のスマホ）に及ぼす影響が複雑に絡み合っているような場合に特に有効です。

パス解析と重回帰分析の違い

パス解析と同じような分析手法として重回帰分析があります。
重回帰分析は1つの目的変数を2つ以上の説明変数で説明をする分析手法です。

先ほどの例でいえば、スマホの人気度（目的変数）を

• 提供するキャリア
• サイズ

などのように相関しない複数の要素（説明変数）で説明できるような場合、重回帰分析が適しています。

重回帰分析でも、1つの目的変数に対する各要素との因果関係の重みを算出することはできます。しかし、変数ごとに相関関係が生まれるモデルには不適な場合があります。

加えて、パス解析では変数間の相関関係を元に目的変数を予測しますが、重回帰分析で注目するのはあくまでも変数間の因果関係です。

パス解析		重回帰分析
扱える	説明変数の相関	扱いずらい
因果関係、 相関関係	説明できる関係性	因果関係

因果関係と相関関係の違いは、原因と結果を明確に説明できるどうかです。

因果関係は必ず原因と結果があり、それらをひっくり返して説明することはできません。 一方相関関係では、1つが変化すれば応じてもう1つも変化するという関係性を示します。

したがって、相関関係は因果関係の必要条件であって十分条件ではないと認識しておくとよいでしょう。

パス解析ではすべて観測変数をあつかう

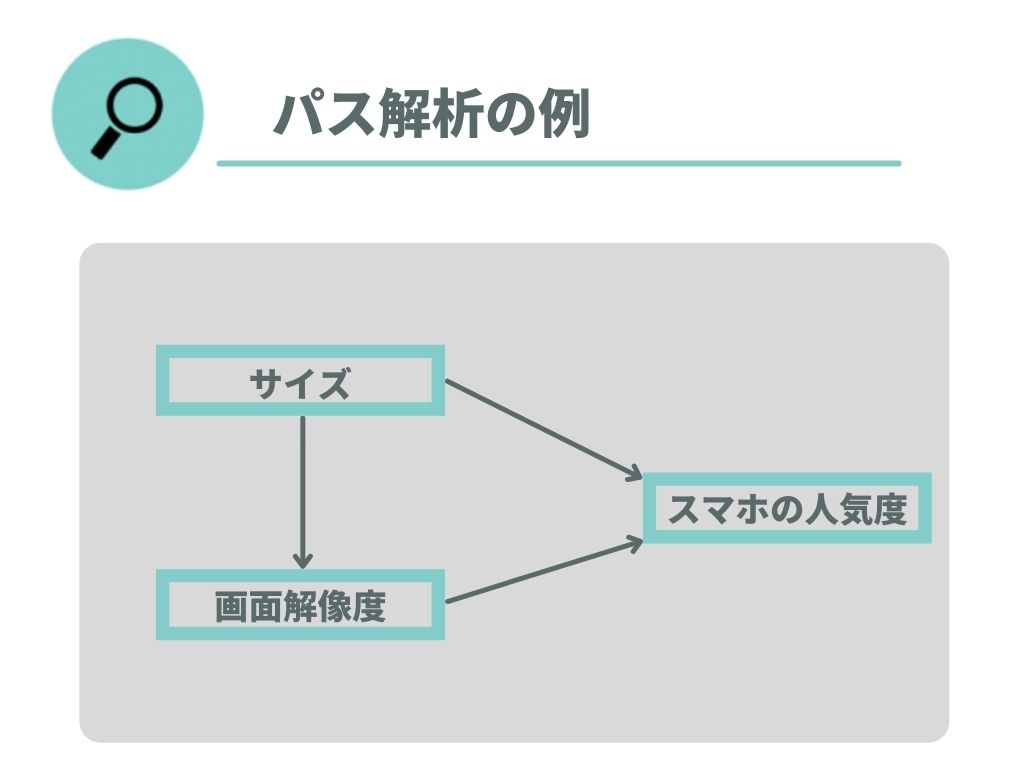
パス解析は、全て観測変数で作成されています。 観測変数とは直接的に観測することのできる変数です。観測変数とはサイズや解像度といったように、リサーチやアンケートで直接回答を得られるものです。

対して共分散構造分析や因子分析では、潜在変数と呼ばれる変数を扱います。潜在変数とは、数値では測ることのできない新たな項目であり、分析者により命名されます。

潜在変数は、パス解析では用いることができません。 共分散構造分析であれば潜在係数を扱えるため、パス解析は共分散構造分析モデルの元になったものと表現されることがあります。

パス図とは

パス解析の「パス」とは何なのでしょうか？

「パス（path）」とは英語で、軌跡・方向・進路を意味します。パス図では相関・因果関係の「方向」を示すものとして扱われています。

パス解析（と共分散構造分析）では変数の相関関係や因果関係をわかりやすく図式化する「パス図」が使われます。 パス図により、説明変数の個数と相関性をわかりやすく表現することができます。 パス図には一定のルールがあります。 このルールが分かると、一気にパス解析の結果表を読み解きやすくなります。

パス図の書き方

パス図の基本形は以下の4つです。

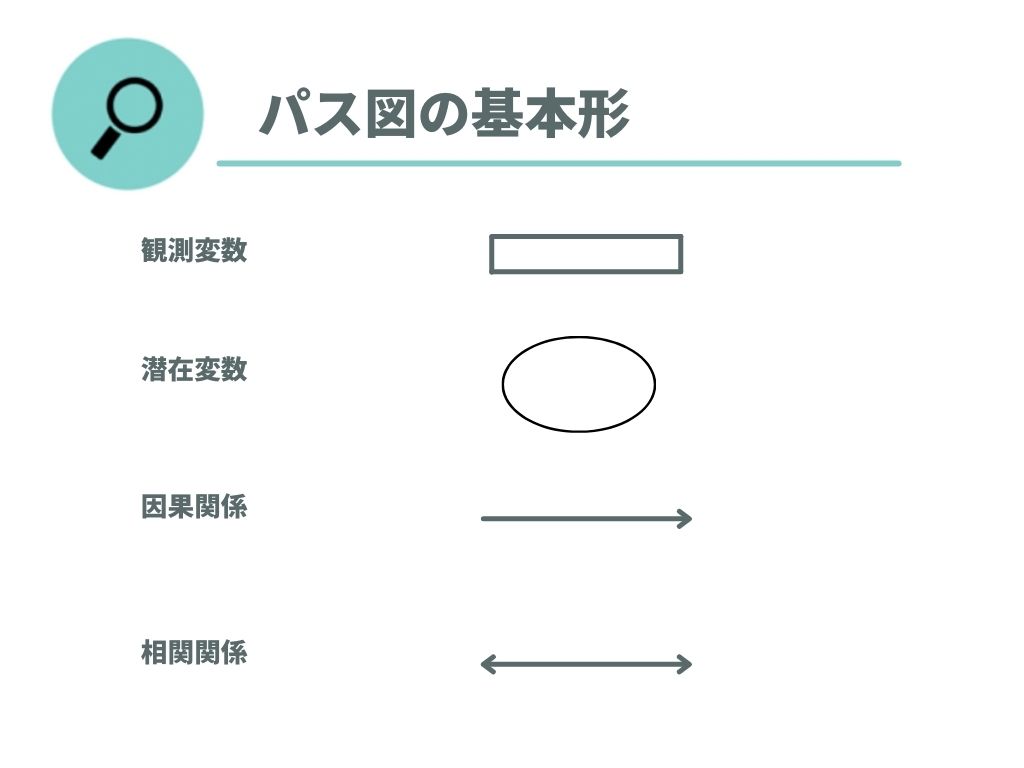
パス図では、観測係数を長方形で書くようにします。また、潜在係数は楕円形で表現します。
片方向矢印は根元が原因を示し、矢印の先が結果を示します。このため片方向矢印は因果関係を表すと認識しておくと良いでしょう。

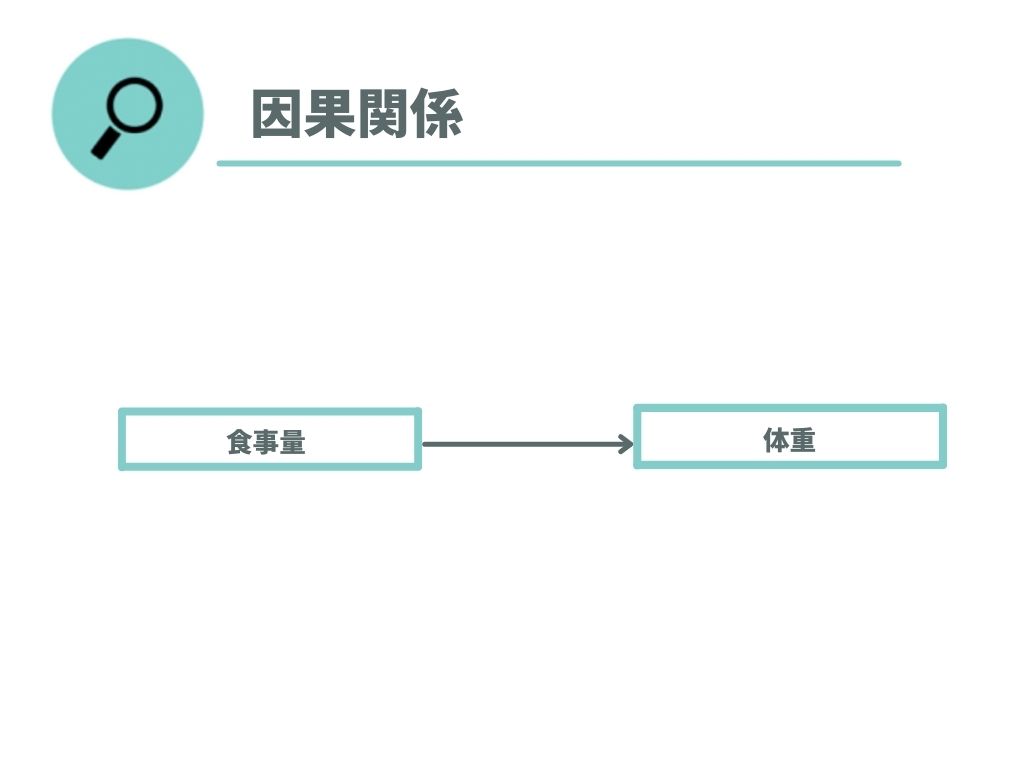
双方向矢印は、相関と呼ばれています。相関とは、片方が増えればもう片方も増える。片方が減ればもう片方も減るといった関係性のことです。双方向矢印はパス解析・共分散構造分析で利用されます。

このとき、相関関係であれば相関係数を記載し、因果関係であれば標準偏回帰係数を記載するというルールがあります。

単回帰分析・重回帰分析・共分散構造分析とパス解析

パス解析を理解する上でややこしいのは以下4つの違いです。

れぞれを図式化すると以下のようになります。

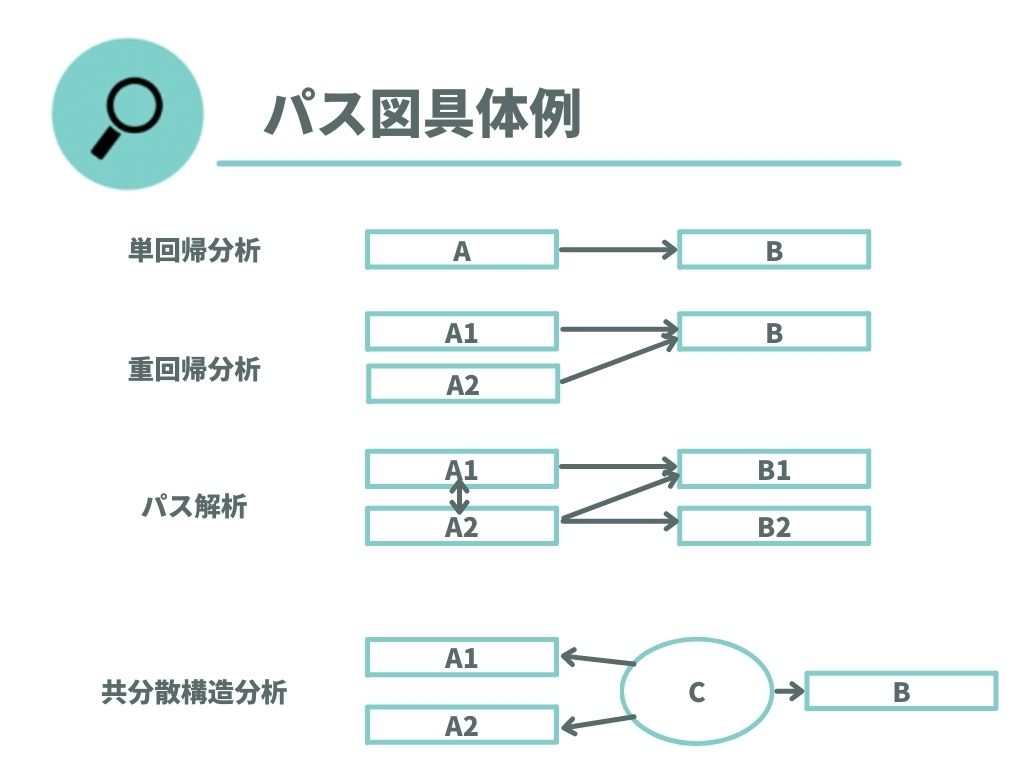
この図は、説明変数と目的変数を表します。 説明変数とは事象の原因となっているもののことで、目的変数とは説明変数によって生み出された結果のことです。

単回帰分析では、目的変数（矢印の先）に対する説明変数（矢印の根）は1対1で対応しているのに対し、重回帰分析では説明変数が2つ以上です。

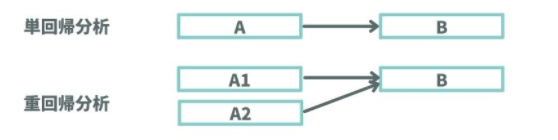
つまり、説明変数が1つか複数なのかによって、単回帰分析になるのか重回帰分析になるのかが分かれていることが見てわかります。 パス解析と共分散構造分析では楕円形（＝潜在変数）があるかないかが大きな違いです。

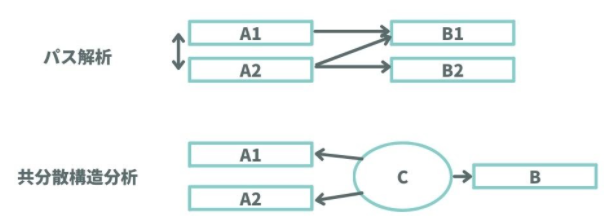
パス図では、長方形を観測変数とし、楕円形を潜在変数と定義していました。 潜在変数があるか否かがまさにパス解析と共分散構造分析を使い分けるポイントです。

共分散構造分析とは

共分散構造分析は、多変量解析の一種。「データサイエンス」のデータ解析でも利用されるだけでなく、心理学、哲学などの分野でも使われているとても重要なキーワードです。 多変量解析とは、違いに関連のある莫大なデータを要約したり、データを解析して未来の予測をしたりする方法です。このため、共分散構造分析はマーケティング分野でもよく利用されています。

◆共分散構造分析がマーケティングで用いられる例

共分散構造分析を実施すると、目的変数と説明変数との因果関係の向き、各要素の重みが明らかになります。

このため、上記の例では分析のフロー（３）で共分散構造分析を利用することができます。 今回は、「ブランド」「デザイン」「コンパクト」「最新機種」「商品の価格」「顧客の住居からの距離」という6つの観測変数を説明変数としていますが、「デザイン」「コンパクト」は「スタイリッシュ」という1つの説明変数にまとめられるかもしれません。

「スタイリッシュ」はアンケートで実施していない項目であり潜在変数です。このように実施したアンケート内容を分析してまとめ直すことができます。

「デザイン」「コンパクト」をまとめて1つの「スタイリッシュ」という説明変数にするためには、因子分析を利用します。

このように、共分散構造分析は主成分分析や因子分析をその内部に含む可能性があります。 そのため、共分散構造分析は、パス図を利用したパス解析よりも見やすく、多くの情報を網羅した図式としてマーケティング分野でも利用されているというわけです。

実際のパス解析事例

実際にパス解析の事例を確認してみましょう

 

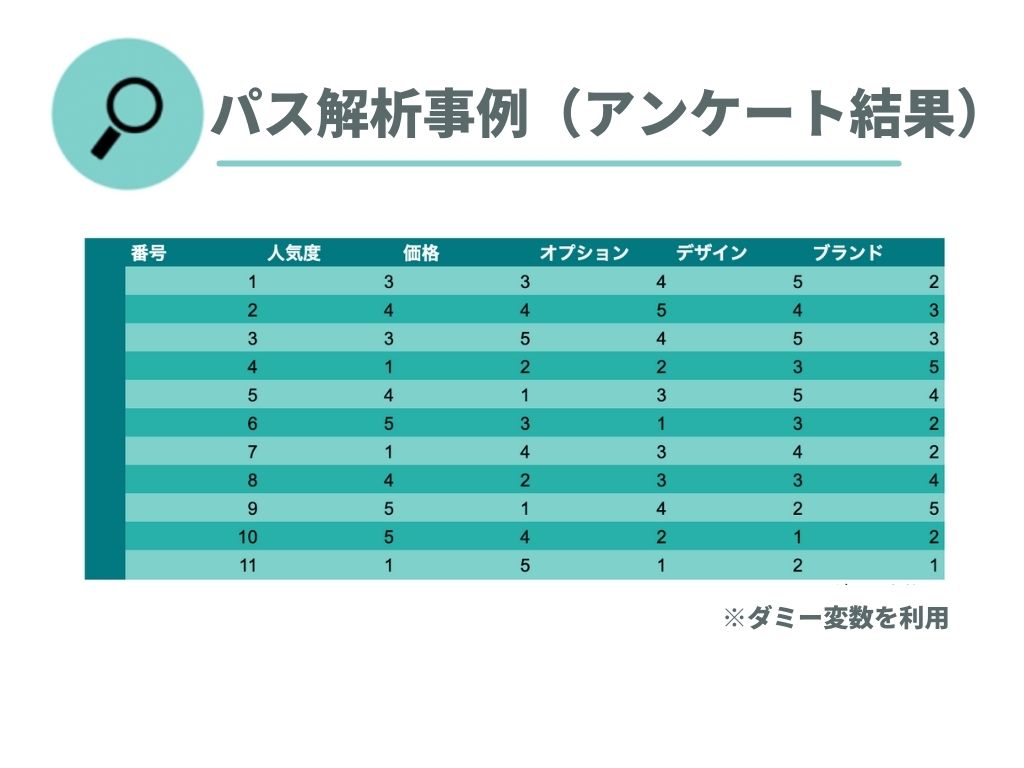アンケートを実施したところ、上記のようなエクセルの結果にまとめられました。 （なお、全ての項目ではわかりやすいように、1がマイナス評価、5がプラス評価となるようなダミー変数を利用してアンケートを実施したと仮定します。）
上記データをパス解析し要因を分析した結果、以下のようなパス図が描けたとします。

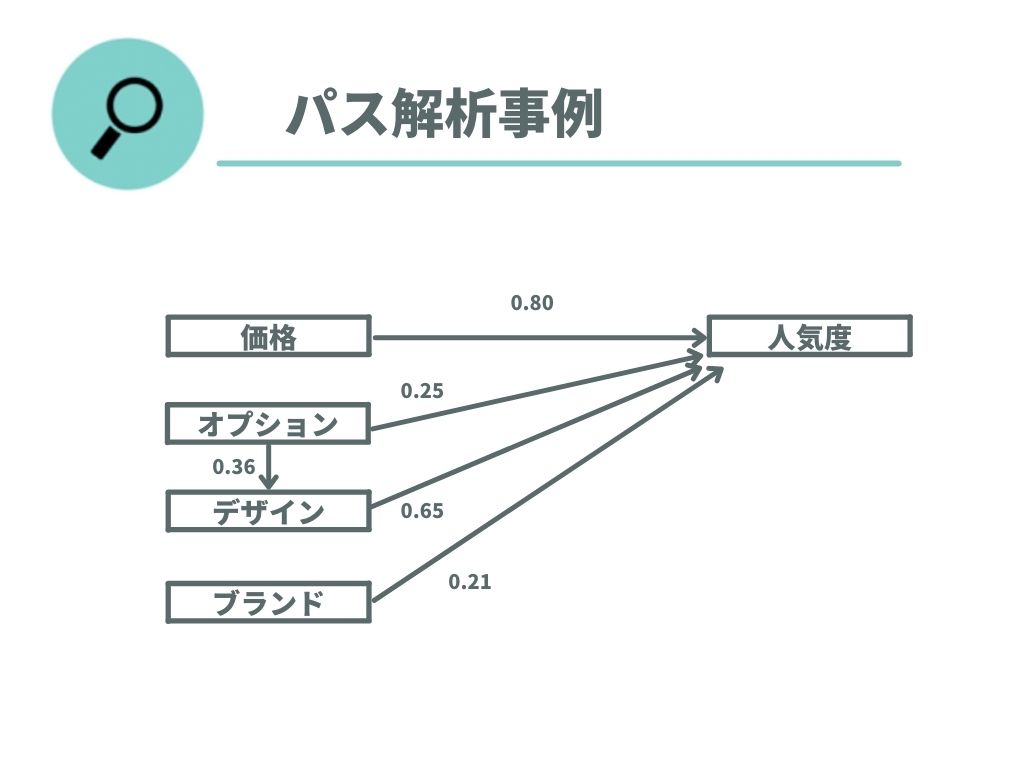
このパス図から以下のような情報が読み取れるでしょう。

この結果から、「より安価なもので他社との優位性を築き上げる」という戦略も取れますし、逆に「ブランド価値向上を狙ってブランディングに力を入れる」という企業戦略も立案できそうです。

パス解析の注意点

パス解析においては以下の２点を注意しましょう。

因果関係の向きを間違えない

制作者によってパス解析の図式は変化することもあります。 例えば、上図では、「オプションがつけばデザインも改善するだろう」という想定の元矢印の向きは、「オプション」→「デザイン」の順序になっています。

しかし、「デザインが良くなればなるほどオプションも改善する」という表現をすれば、「デザイン」→「オプション」という順序に変わります。

この順序は商品によって変化することがあります。 したがって、パス解析をする場合には、因果関係は図の通りで間違っていないのかを確認する必要があります。

パス図の誤差

パス図を使って因果関係を表現をするとき、誤差を考える必要があります。

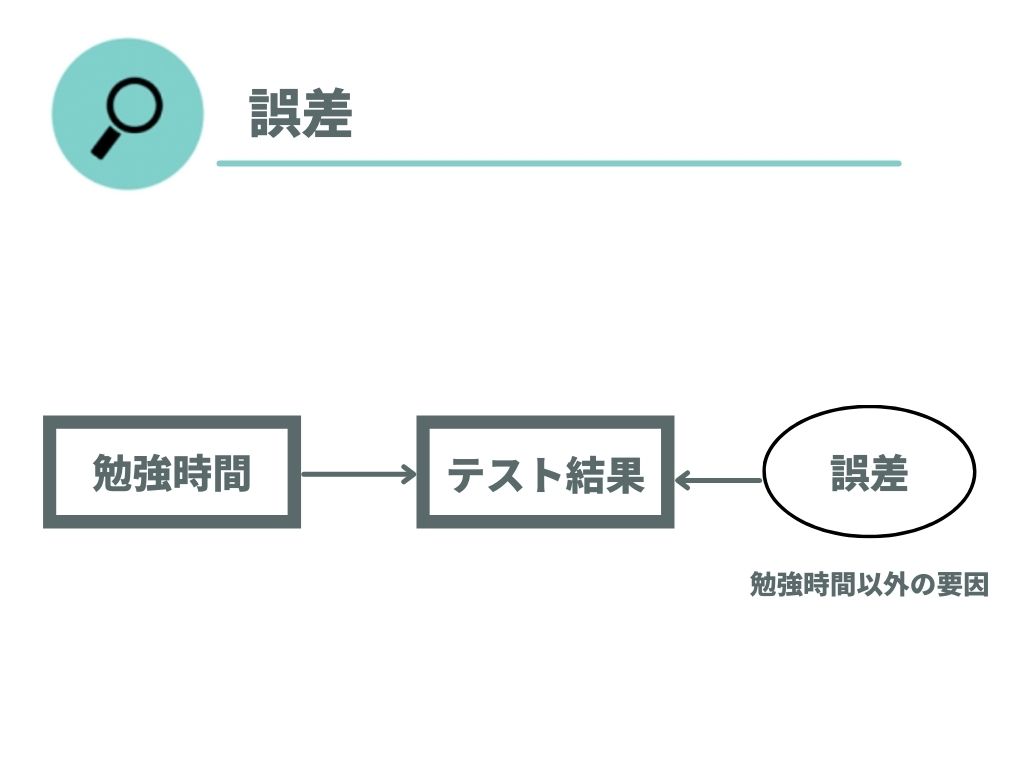
例えば、勉強時間とテストの点数の関係性を描くとしましょう。このとき、原因が勉強時間で結果がテストの点数と考えることができます。 ただし、このときテストの結果の原因として勉強時間のみを想定することはできません。 環境やもともとの集中力などといった他の要素も関わってくるものです。

このように説明変数以外に影響を及ぼす要素をパス図では誤差として表現します。

パス解析を実施するには？Amos、SPSS、R、Pythonについて

パス解析では、Amos（共分散構造分析ソフト）やSPSS、R、Pythonなどが利用されます。 中でもRはデータ分析に特化した言語です。多くの分析に適用できるため、初めてパス解析や共分散構造分析を実施するという方はRを使うという方も多いです。

RはPythonよりもわかりやすい構造のため初学者におすすめですが、その後機械学習やディープラーニングに進んでいきたいという方は、始めからPythonを勉強しておくのが良いでしょう。

パス解析や共分散構造分析では非常に膨大・高度な処理をするため、こうしたプログラミング言語とは相性が良いのです。

まとめ

本記事ではパス解析について解説しました。 扱うデータ量が増えれば増えるほど、データの可視化の必要性は高まります。 特に複雑なモデルになった際は、パス解析を利用して見える化することで、自社の今後のプロモーション・マーケティングにデータをより活用させることもできるでしょう。