主成分分析とは?因子分析との違いや事例を初心者にも分かりやすく解説
2021年09月29日

主成分分析は、アンケート調査や市場調査を実施する上で有効な分析手法の一つです。 特に、商品やサービスの評価分析や顧客満足度が高い店舗の特定などに役立ちます。
しかし主成分分析はとっつきにくい用語も多く、敬遠している人が多い手法でもあります。 しかも、同じ多変量解析の一種である因子分析・クラスター分析と混同している人も多いようです。
この記事では、統計学初心者の方にもわかりやすいように主成分分析の概要や手順、因子分析やクラスター分析との違いを解説します。
主成分分析とは
- 主成分分析とは
- たくさんの変数を少ない変数に置き換え要約することで、データを理解しやすくする分析手法。 主成分分析では、データを1〜3つの変数(=主成分)に置き換えることが一般的です。
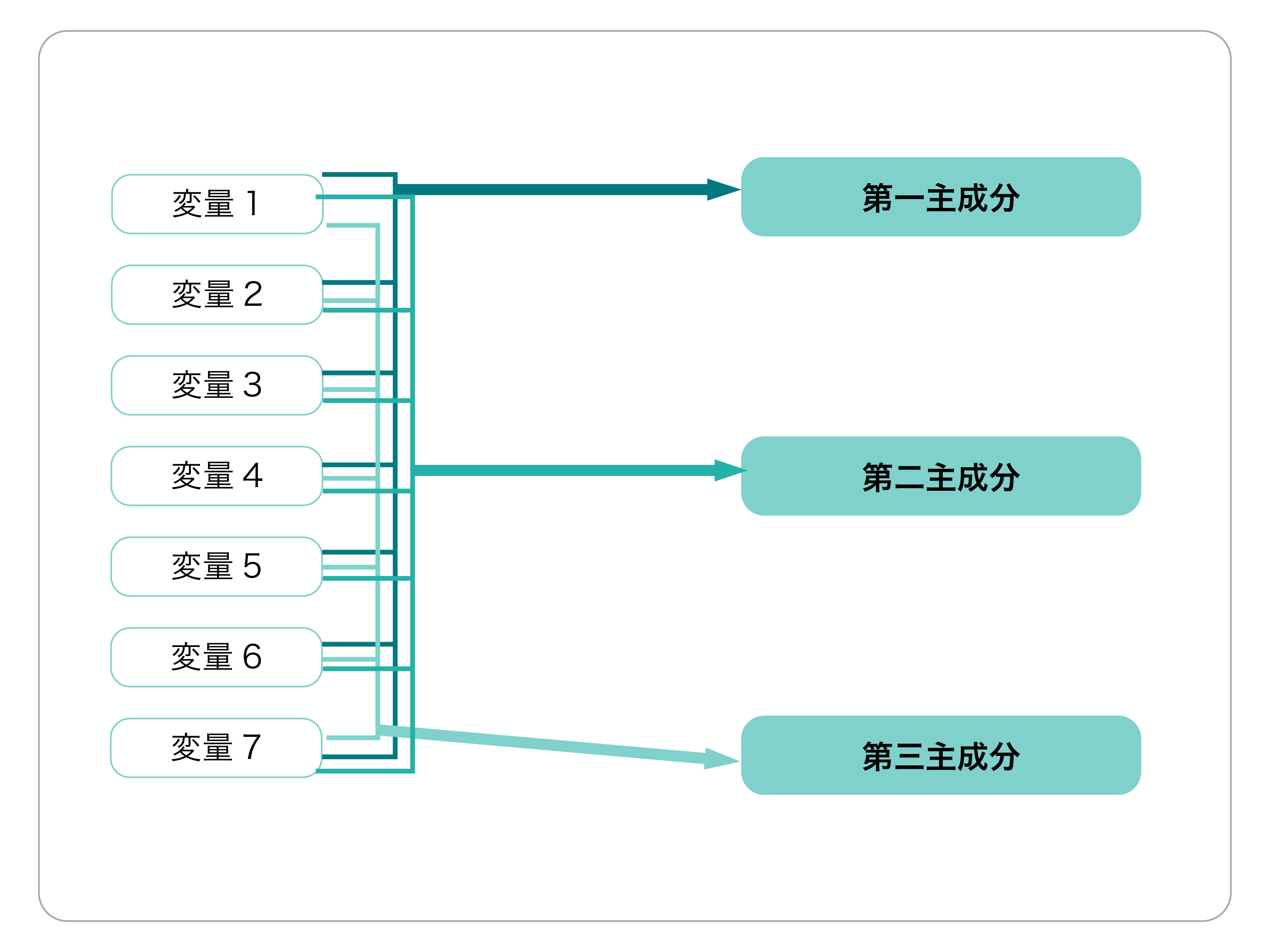
主成分分析は、分析対象の総合力を把握し総合力トップを選出したいような場合に使われることの多い分析手法です
例えば、以下のようなシーンで特に有効です。
- 店舗分析
- 飲食物や作品の総合評価
- 成績分析
データを置き換えるとき新しく作られた変数を「主成分」と呼びます。最初に求められるものから順に第一主成分、第二主成分、第三主成分…と呼ばれます
その中でも第一主成分は、一般的に分析に使用した対象の総合力を示します。
これは第一主成分が分析に使用したそれぞれの変数を合成して作られたもの(主成分)の中で、最も多く元のデータを反映しているためです。
第一主成分の定義は、分析者により、テストの総合成績・店舗の顧客満足度など変化します。
例えば複数店舗を持つ飲食店であれば、顧客アンケートにより集めた「接客の質」「店舗の雰囲気」「過ごしやすさ」「メニューの豊富さ」「メニューの味」「価格」といった変数を利用し主成分分析を行うことで、総合力を算出できます。
その結果、顧客満足度の高い店舗を見つけ出すことが可能になります。
ただし、このときどんな変数を選んでも総合力が求められるわけではありません。
例えば、生徒の試験での総合成績を出したい場合に「国語」「数学」「英語」といった教科の他に、全く関係のない「身長」「体重」「髪の毛の長さ」といった項目を分析しても、精度の高い総合評価が導き出されません。
したがって主成分分析では、ある領域に関する総合力の要素として適した変数を分析者の判断で集めて分析することで、総合力を求めます。
主成分分析の活用事例
主成分分析はビジネスシーンだけでも様々な活用ができる汎用性が高い分析です。 主成分分析が活用されている事例を3点紹介します。
活用1.顧客満足度の調査
主成分分析の活用事例の一つ目は、「顧客満足度の調査」です。
主成分分析により「商品の質」「価格」「接客態度」といった項目から、総合的な顧客満足度が算出できます。
総合的な判断のほかにも、どの要素が顧客満足度に最も影響しているかを把握できるため、戦略立案にも役立ちます。
例えば、顧客満足度を上げるには接客の質の向上が必要だと考え、接客部門の採用強化を検討していたとします。
しかし主成分分析の結果、顧客満足度は商品の質に左右されていると判明したとしましょう。 このような場合は、接客部門ではなく製造部門の採用を強化するなど、顧客満足度を上げるための最適な施策を実行しやすくなります。
つまり主成分分析は顧客満足度を知る目的以外にも、今後の方針を決める際にも活用できる分析だといえます。
活用2.作品・製品評価
主成分分析は商品を紹介するメディアや、製造メーカーを中心に、「作品・製品評価」にも活用されています。
新聞や口コミサイトで見かける総合ランキングも、主成分分析が活用されていると考えられます。
他にも代理店や商社のように、自社商品ではない商品を扱う企業でも、主成分分析は活用可能です。 具体的には、自社が今販売している商品それぞれの総合評価を知ることで、顧客が今求めている商品が把握できます。
そして該当商品を積極的に販売することで、顧客満足度は上がり、継続的な契約やクロスセル・アップセルにも繋がると考えられます。
活用3.人事評価や人員配置
マーケティング領域の他に、人事領域でも主成分分析は活用できます。
例えば新規立ち上げ部署のマネージャーを選出したい場合、「これまでの実績」「立ち上げ分野に関する知識」「上司からの評価」「部下からの評価」「部下の実績」といった項目を変数とし主成分分析を行うことで、総合力が高く最もマネージャーにふさわしい人物を選出可能です。
また、人事評価でも上記同様に様々な変数を集めて主成分分析を行うことで、対象者を客観的な視点で評価ができます。
加えて総合力を上げるために影響が大きい要素も分かるため、教育や研修にも活かせるでしょう。
主成分分析のメリット
主成分分析を実施するメリットは、主に以下の2点です。
- データ数を少なくし、調査を効率化する
- 総合力に影響している項目の把握ができる
メリット1.データ数を少なくし、調査を効率化する
主成分分析のメリットとして、変数をまとめることで分析者が扱うデータ数が少なくなるために調査査結果が格段に理解しやすくなることが挙げられます。
それにともない解釈もより短い時間で行えるため、分析を効率的に行うことができます。 データが少なくなることで、計算する際のシステムへの負荷や所要時間の減少も期待できます。
メリット2.総合力に影響している項目の把握ができる
主成分分析では、対象データの総合力そのものだけでなく、総合力に影響している項目まで把握できるのもメリットです。
総合力に影響を及ぼしている項目が明らかになることで、売上アップ・利益拡大に寄与する施策が効率的に打ちやすくなるでしょう。
主成分分析のデメリット
主成分分析を実施する上でのデメリットは、主に以下の2点です。
- 取りこぼされる情報が出てしまうこと
- 分析の内容が分析者の判断に依存すること
デメリット1.取りこぼされる情報が出てしまうこと
主成分分析はデータを要約する分析であることから、どうしても取りこぼされる情報が生じます。
そのため、主成分分析によって生成された新たなデータのうち、元の情報がどれだけ反映されているかを確認する必要があります。
(どのように確認するかは、次章の”寄与率”の項にて詳しく解説します。)
デメリット2.分析内容が分析者の判断に委ねられる
主成分分析におけるもう一つのデメリットは、分析内容が分析者の判断に委ねられる点です。具体的には以下の3点で分析者の判断が必要です。
- 分析対象とする変数の設定
- 第一主成分における定義
- 第二主成分以降の意味づけ
まず分析の対象とする変数が、分析者の判断により選定されます。
例えば、第一主成分を書籍の総合評価と定義したい場合に、変数として「著者の信頼性」「内容の充実度」といった一般的なもののほかに「帯にある推薦者のコメント」といった一見内容とは関係がなさそうなものを選んだとしても、分析者が有効と考えるのであれば分析に入れても問題がないのです。
次に総合力を示す第一主成分において、「何に関する総合力とするのか」という定義も分析者が決定します。第二主成分以降でも、分析者自ら意味付けを行います。 (ちなみにこのとき、総合力を示す第一主成分以外の主成分は、第二主成分が理系能力、第三主成分が文系能力…というように、相反する内容にするというルールがあります)
このように、主成分分析では分析者によってデータの持つ意味合いやそもそもの分析の定義が変わるため、分析者の責任や仮説の重要性が比較的大きい分析手法といえます。
主成分分析に関する用語解説
主成分分析の手順を紹介する前に、前提知識として主成分分析に関する用語を解説します。/p>
主成分と主成分得点
- 主成分
- 分析対象の各データを統合して作られたデータのこと。
- 主成分得点
- 主成分を表す軸における一つひとつのデータ座標のこと。
主成分分析では総合力を示す第一主成分だけでなく、説明変数の数だけ主成分が生成されます。この時、最初に求められた主成分から順に、第一主成分、第二主成分と名付けられます。
分析者があらかじめ定義した総合力を示すのは第一主成分のみで、第二主成分以降については分析後に結果を見て、分析者がどのようなことを示しているデータか解釈する必要があります。
また主成分分析では分析結果をわかりやすく図式するため、下図のように散布図上のデータの分散が最も大きいところに軸を通すことがあります。その際はこの軸が主成分を表します。
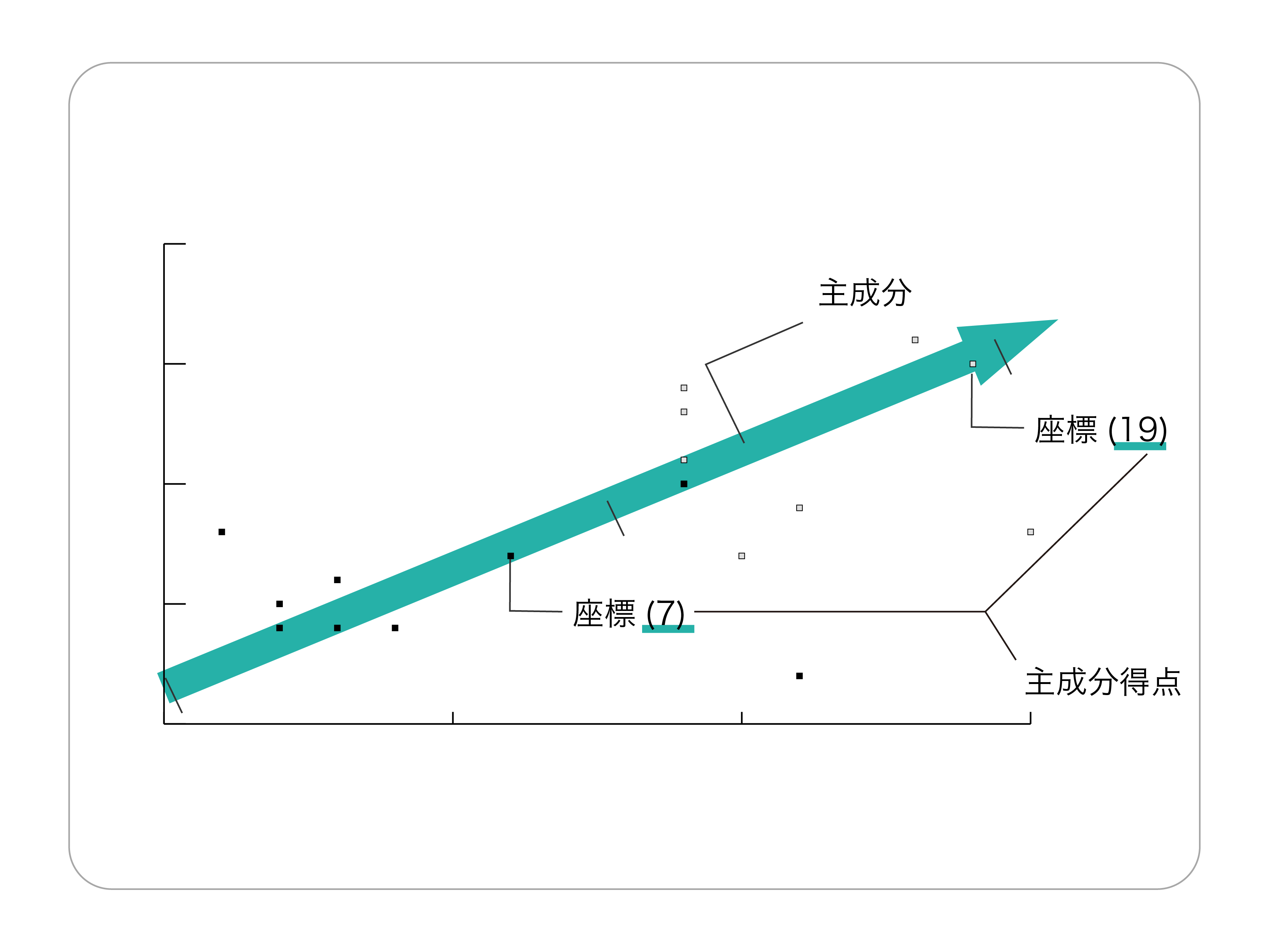
そして、この主成分を表す軸における一つひとつのデータ座標を主成分得点と呼びます。
この主成分得点が最も大きい個物が、分析者が定義した総合力で一番高い個物を示します。
データの標準化
- データの標準化
- データの尺度を揃えるためにデータを平均0、分散1となるように変換すること。
主成分分析の場合はデータの標準化がされていなくても分析自体はできますが、尺度を揃えた方が計算・分析が効率的にできるため、標準化をして分析に取り組む場合が多いです。
固有値
- 固有値
- 主成分分析においては、主成分の分散を指す。
固有値の値が1を切る主成分の場合は、結果への影響が少ないと考えられ分析する必要がないとされ、算出されたとしても分析には利用しないこともあります。
固有値ベクトル
- 固有値ベクトル
- 主成分と、分析対象とした元のデータの変数との相関係数を指します。
あらかじめ定義してる第一主成分以外の主成分が何を表すかを解釈する時の手がかりとしても使えます。 固有値と混同しないように注意が必要です。
寄与率
- 寄与率
- 対象とする主成分に、元データの情報がどれだけ反映されているかを表した数値のこと。
- 累積寄与率
- 各主成分の寄与率を合計したもの。
累積寄与率は、高ければ高いほど情報の取りこぼしが少ないことを表します。
精度の高い分析が行えることから、累積寄与率は高いほどよいとされています。
寄与率の基準は特に定められていないものの、分析の精度を担保する上でも最低でも情報の半分は反映したデータを検討するべきです。 第一主成分と第二主成分の寄与率の合計で50%を一つの目安とするとよいでしょう。
主成分分析の手順
ここからは実際に主成分分析を行う手順を説明します。
【準備】主成分分析でよく使われるソフト
実際に主成分分析を行う際には、ビジネスの場でも多く使われるExcelに統計解析用機能を追加できるExcel統計や、フリーソフトのRが使われることが多いです。 ここからは、Excel統計での分析を中心に解説していきます。
1.主成分を定義する
まず最初に、主成分をどう定義するかを決めます。
何を第一主成分と定義するかは、主成分分析を活用したいシーンや使用するデータによって分析者が決定する必要があります。分析に使用するデータから導き出される総合力としてふさわしい内容を、第一主成分として定義しましょう。
ここでは例として総合力を示す第一主成分を、ある飲食店における顧客満足度として定義します。 他にも、映画の総合評価や、ある人物の総合成績などが第一主成分の定義の代表例として挙げられます。
2.主成分と主成分得点を求める
続いて、主成分と主成分得点を求めます。
今回の例では主成分のうち、第一主成分は「ある飲食店における顧客満足度」と定義します。その上で第一主成分における主成分得点をもとに、一番高い総合力を有する飲食店を算出します。 主成分Zは「Z=a₁y₁ +a₂y₂ + …aₚyₚ」の式で表せます。y₁ , y₂は各説明変数の基準値、a₁ , a₂は各説明変数が主成分に与える影響の度合いを示します。
「ある飲食店における顧客満足度」を主成分とする場合、y₁ , y₂は「接客」や「料理の美味しさ」の基準値を代入することとなりますね。 しかし基本的にはソフトが計算するため、上記のような計算式を実際に使うことは少ないでしょう。
Excel統計の場合は、以下手順で行います。
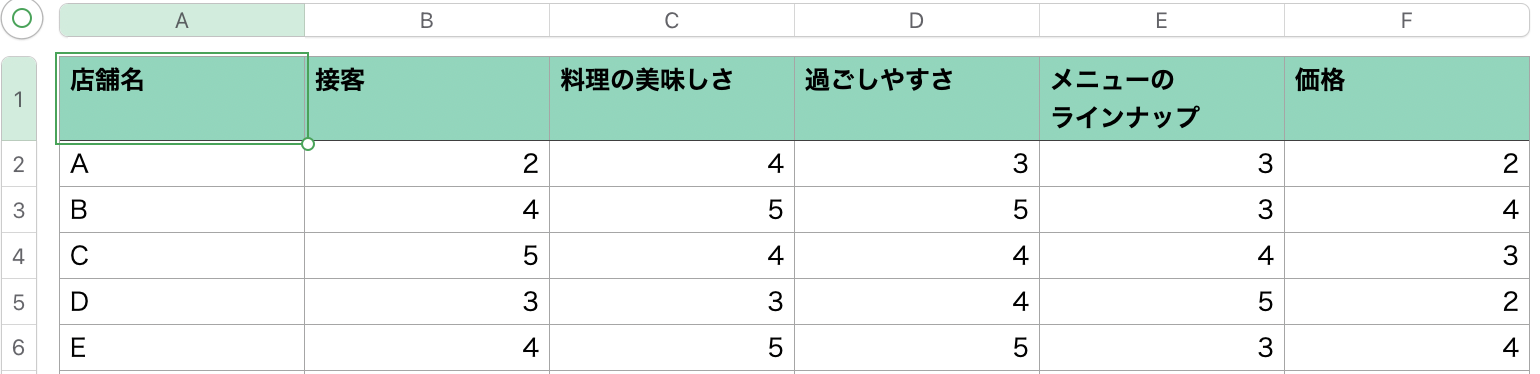
- まず、分析するデータをExcelシート内に用意します。
- 分析するデータを指定。まず分析したいデータのうち、今回分析したい題材となる部分のラベル(A1)を選択しましょう。その後、各変数のラベル(B1〜F1)をControlキーを押しながら選択します。
- メニューから「Excel統計」→「多変量解析」→「主成分分析」を選択します。
- オプションタブから「線形結合している変数を除いて分析する」「標準化したデータの分散共分散行列(相関行列)から計算する」「主成分得点を出力する」にチェックし、OKをクリック。分析が実行されます。
- 出力された結果を確認しましょう。
3.分析の精度を確かめる
主成分分析の精度は寄与率・累積寄与率を用いて確認しましょう。
- 寄与率
- 主成分に元のデータの情報がどれだけ反映されているのかを表した数値。
- 累積寄与率
- 寄与率を合計した数値 (例:第一主成分の寄与率53%、第二主成分の寄与率28%であった場合、第二主成分までの累積寄与率は81%で、「第一主成分と第二主成分には元のデータのうち81%の情報が反映されている」といえる)
出力された結果の「固有値表」の部分より、寄与率・累積寄与率が確認できます。 主成分分析では一般的に第二主成分得点までをグラフにするため、第二主成分までの累積寄与率を分析精度を測るのが一般的です。
寄与率・累積寄与率は高ければ高いほど良いとされていますが、明確な基準は決められていません。 しかし最低ラインとして、第二主成分までの累積寄与率が50%を超えているかが目安となります。 あまりにも累積寄与率が低い場合は、分析対象の選定や第一主成分の定義など見直す必要があります。
ちなみに、累積寄与率と分析対象の変数の数は相関関係にあることが多く、分析対象の変数が増えるほど、累積寄与率は下がる傾向にあります。
累積寄与率が50%を切る場合は、1.5倍の寄与率を目指すのであれば変数をもともと使っていた数の6割まで減らしてみるなど、分析対象の変数を目指す寄与率に合わせて減らして再分析してみるのも一手です。
3.分析結果を検討する
主成分分析の精度に問題がなければ、分析結果を視覚的に分かりやすく示すためにグラフを作成します。 グラフは「主成分得点」と「固有値ベクトル」の2点を作成します。
<主成分得点グラフの作成方法>
分析の結果求められた第一主成分得点と第二主成分得点をもとに、横軸を第一主成分(Z1)、縦軸を第二主成分(Z2)としてグラフを書きましょう。
<固有値ベクトルグラフの作成方法>
最大の固有値、2番目に大きい固有値、それぞれに対応する主成分の固有値ベクトルの値をもとに、固有値ベクトルグラフをを書きます。
主成分得点グラフと同様、第一主成分を横軸(Z3)、第二主成分を縦軸(Z4)とします。(縦軸を第一主成分・横軸を第二主成分としても問題はありませんが、主成分得点のグラフと固有値ベクトルのグラフの軸の定義は統一した方が分析しやすいでしょう)
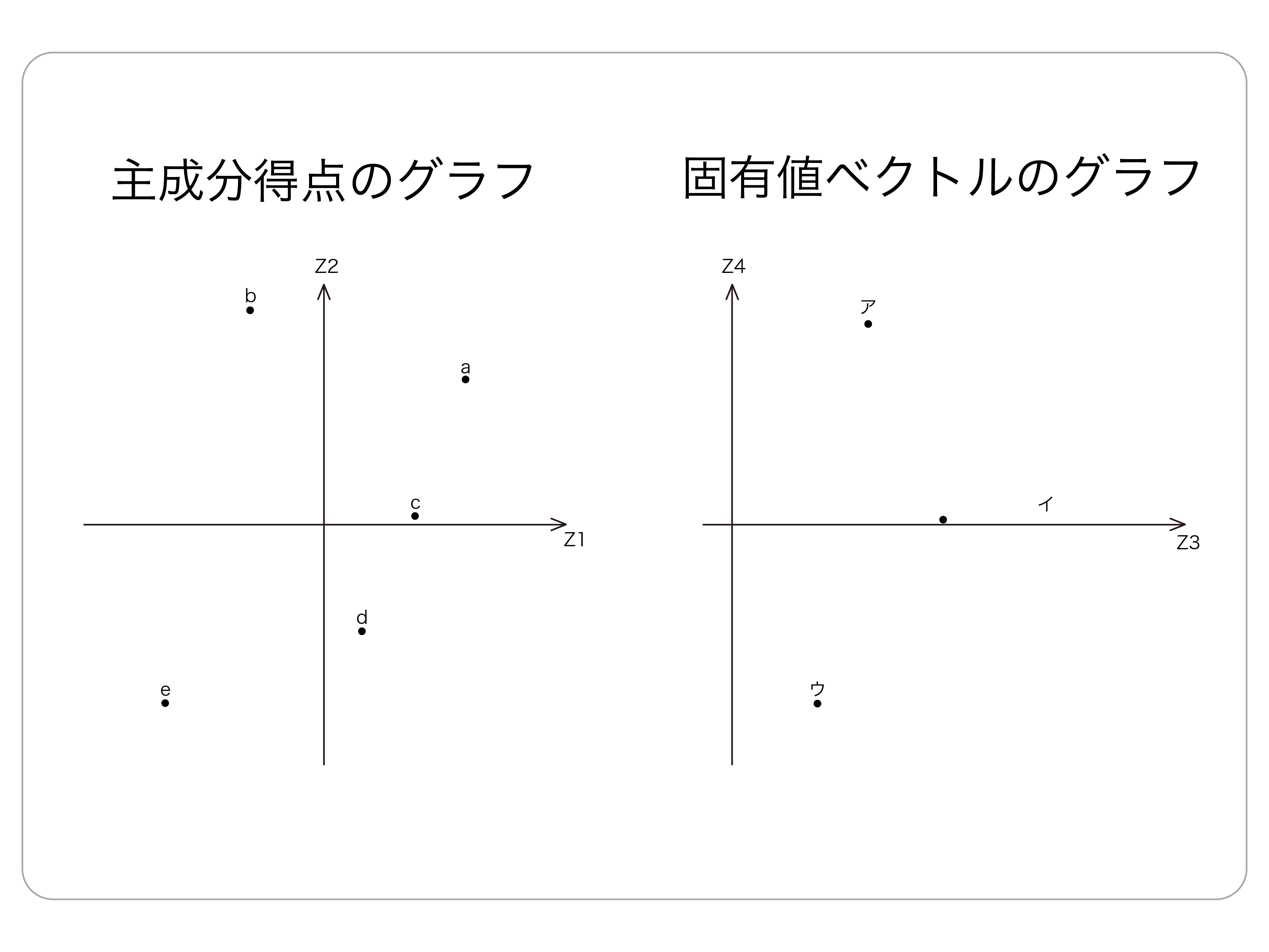
主成分得点グラフの横軸に注目します。
横軸は第一主成分としたため、右にあるデータほど総合力が高いと判断することができます。 つまり、総合力の高い順に並び替えると「a,c,d,b,c」となるのです。
続いて固有値ベクトルのグラフを見ていきましょう。
固有値ベクトルとは、主成分と元のデータの変数の間の相関係数のことでした。つまり、固有値ベクトルが大きいものほど、主成分との元のデータの相関関係が強い、主成分への影響が強い要素だといえます。
固有値ベクトルのグラフにおける横軸は第一主成分に関する値であり、それぞれの変数が総合評価にどの程度影響を与えているのかを把握できます。この値が大きいものほど総合評価への影響力が大きいということです。 この例図の場合はイの要素が最も総合評価への影響が高く、イの要素で高評価を得たものは総合評価も高くなりやすいといえます。
さらに、両方のグラフを見比べてみましょう。
主成分得点グラフのb、固有値ベクトルグラフのアは同じくらいの高さにありますね。この時、bはアの項目に対して評価が高いと判断ができます。
これは、第二主成分との相関関係が高いアの要素で評価されている個体は、第二主成分における主成分得点が高くなるためです。 逆に第二主成分と相関の低く、かつ第二主成分と相反するウの要素で評価されている個体は、第二主成分における主成分得点が低くなります。
上記と同様の考え方で、eも総合評価自体は低いものの、ウの項目の評価は高いと考えられます。 このように主成分得点グラフと固有値ベクトルグラフを活用し、主成分分析で導き出された結果を検討していきましょう。
主成分分析と他の分析方法との比較【因子分析・クラスター分析】
主成分分析と同様に多変量解析である因子分析とクラスター分析。 ここからは、それぞれどんな分析手法なのか簡単に紹介するとともに、主成分分析との違いを解説します。
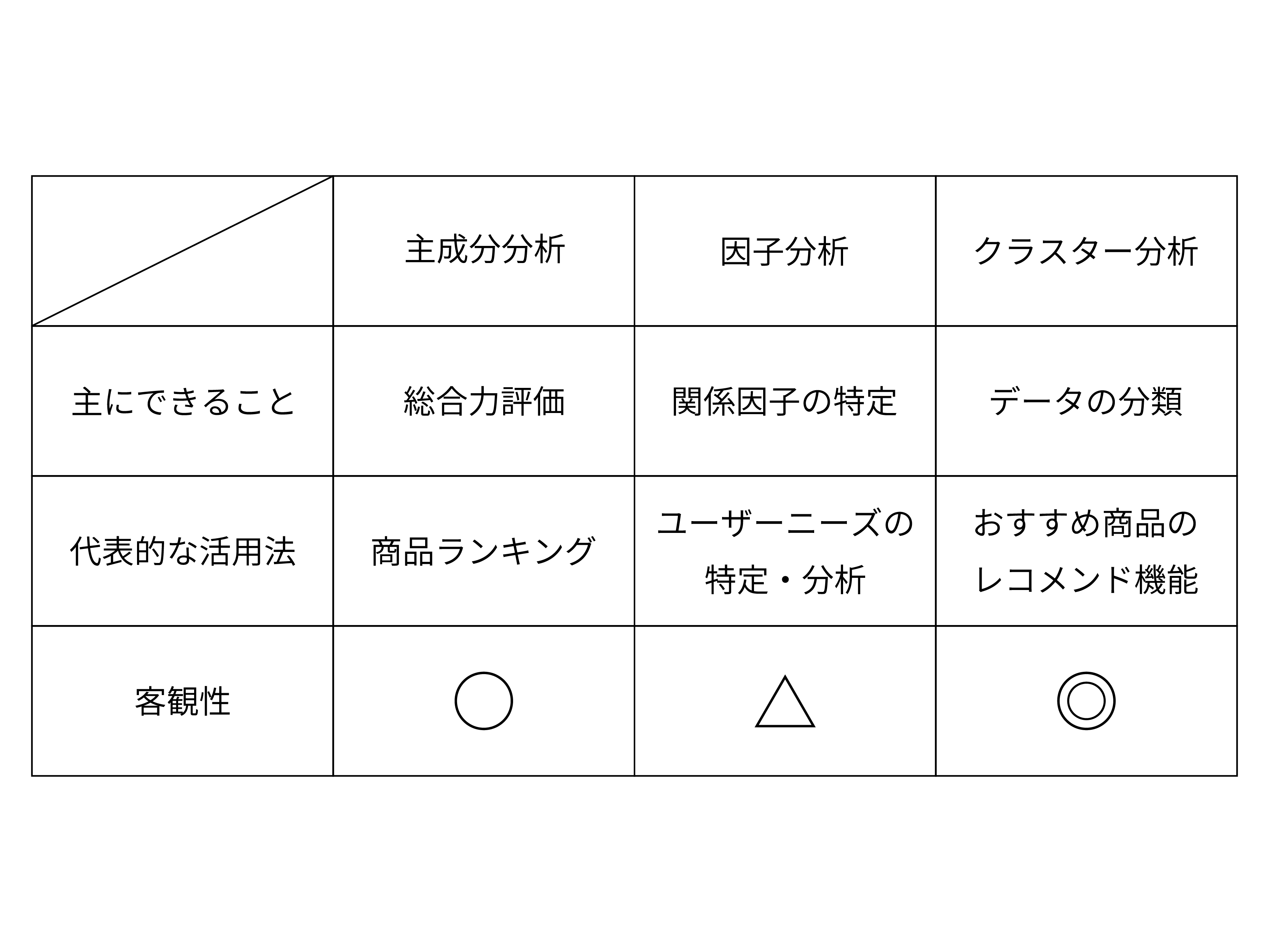
主成分分析と同様に多変量解析である因子分析とクラスター分析。 ここからは、それぞれどんな分析手法なのか簡単に紹介するとともに、主成分分析との違いを解説します。
主成分分析と因子分析の違いとは
因子分析とは、変数の背後にある前提・条件となる潜在因子や共通因子を見つけ出すための分析方法です。 例えば、機能・デザインをリニューアルした商品の売上が低下しているとします。
さらに、口コミ評価で機能面の悪評が増えている場合、売上低下の背後には機能が変わったことへの不満という顧客感情があると考えられます。
しかし主成分分析では、説明変数を基にして目的変数を求めますが、因子分析では、目的変数を基にして説明変数を求めていきます。 つまり主成分分析と因子分析は、データを説明できる要素を新たに作り出すという点においては類似していますが、実際のプロセスや考え方は真逆の分析と言えます。
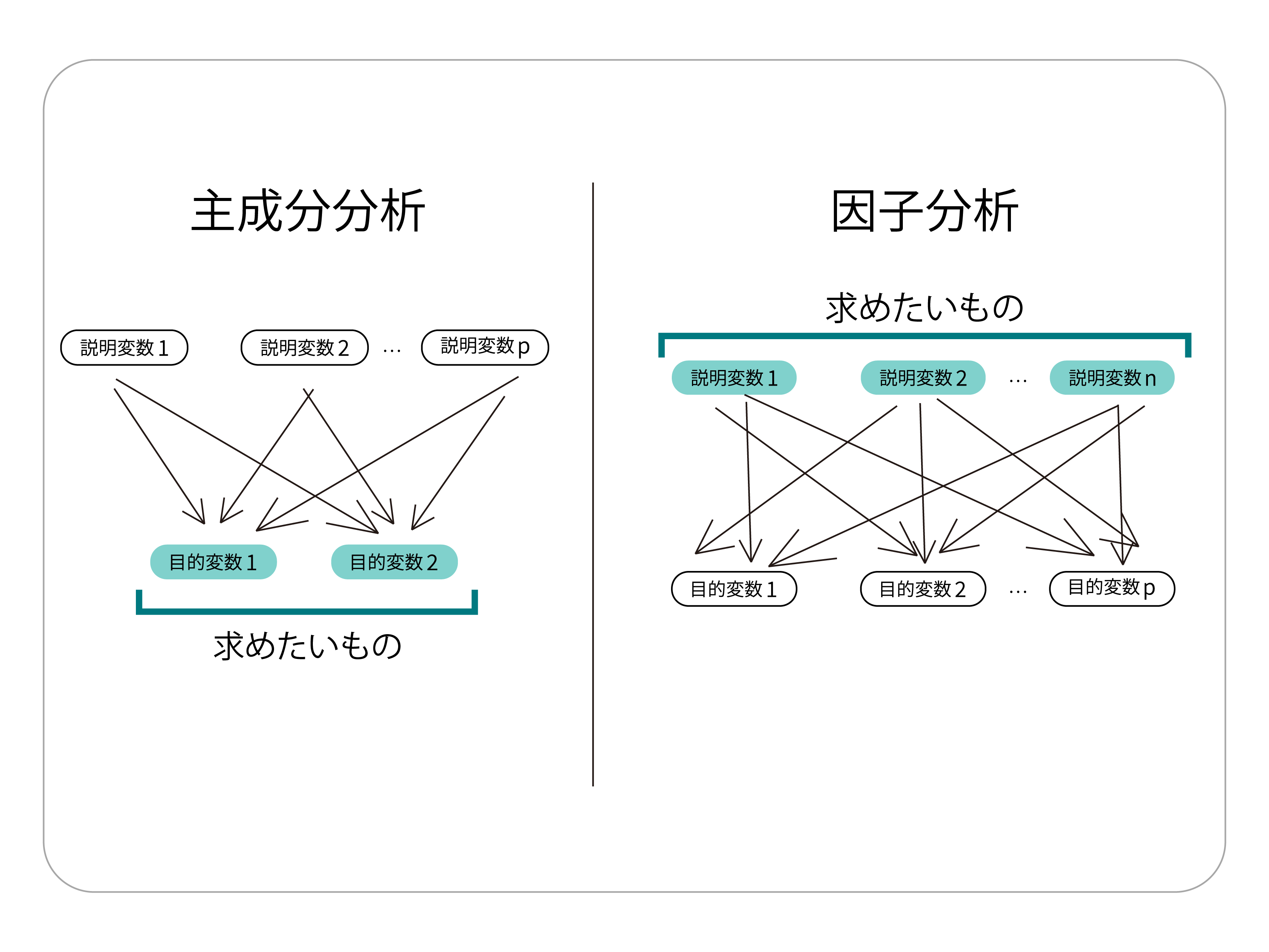
このように、あるデータに関係していると思われる事柄を見つけ出していくのが因子分析です。よって因子分析はユーザーニーズや隠された意図・心理を知るために有効な分析手法といえるでしょう。 主成分分析と因子分析は、どちらも多くの変数を用いて少数の結果を抽出していく点は非常によく似ている分析手法です。
因子分析では、主成分分析よりも分析者の意図が入り込みやすく、客観性に欠けるデメリットがあります。しかしある程度分析者の意図に沿って分析結果が提示できるため、交渉や説得が必要な場面ではメリットでもあります。
よって因子分析は、心理学やマーケティングのように、プレゼンテーションを行う機会の多い分野でよく用いられています。対して主成分分析は、客観性が高い分析方法であるため、物理学や医学といった厳密なデータが求められる分野でも活用されています。
主成分分析とクラスター分析の違い
クラスター分析とは、集団の中から似たものを集めてグループ化する手法です。
グループ化により巨大なデータの解析や特徴の理解が行いやすくなります。 主成分分析とクラスター分析は、膨大なデータを分かりやすくまとめる点は共通しているものの、全体的な分析手法は異なっています。
主成分分析では、分析により変数を圧縮した新たなデータが生成されますが、クラスター分析では新しいデータは生成されず、既存データの分類に留まっています。 こういった特性の違いから活用シーンは異なっており、ビジネス領域においては、以下のような活用方法が一般的です。
- 主成分分析:顧客満足度や商品評価の分析
- クラスター分析:ユーザーをセグメントした上での商品・サービス訴求
クラスター分析は経済学・法学・農学など幅広い分野で使われており、主成分分析よりも客観性の高い分析方法です。
主成分分析も客観性が高い分析方法ではありますが、分析対象の変数や第一主成分の定義・データの解釈など、分析者の主観に依拠する部分も多くあります。 一方クラスター分析は、データ間の距離を分類する分析手法であるため、主観が入りにくく、主成分分析よりも客観性が高い分析方法といえます。
まとめ
ここまで、主成分分析の定義、分析の手順、他の代表的な多変量解析との違い、活用方法など解説してきました。最後に改めて要点をまとめておきます。
主成分分析は、ビジネスシーンにおいて「顧客満足度の調査」「作品や製品の評価」「人事評価や人員配置」といった、マーケティング領域で活用されることの多い分析手法です。マーケティング領域以外にも、人事領域をはじめ様々な領域で幅広くビジネスに活用できます。
最後に主成分分析をビジネスで活用するメリットは、大きく以下の2点が挙げられます。
- データの数が減るためにデータが格段に理解しやすくなる
- 総合力だけでなく、総合力に影響する項目まで把握できる
主成分分析を有効活用して、より的確で顧客に響くマーケティング活動をしていきましょう。
- サービス概要を無料配布中「3分で読めるGMOリサーチ&AIのサービス」
-
GMOリサーチ&AIはお客様のマーケティング活動を支援しており、さまざまなサービスを提供しております。
- スピーディーにアンケートデータを収集するには
- お客様ご自身で好きな時にアンケートを実施する方法
- どこの誰にどれくらいリーチができるか
ぜひこの機会にお求めください。 - 資料請求する


