有意差とは統計学の指標の一つです。

仮説と標本の観察による結果の差が出たとき、その差が「誤差の範囲内」なのか「誤差では済まされない意味のある差」なのかを明らかにする必要があります。

「意味のある差」のことを統計学では「有意差」と表現します。 本記事では有意差の概要や使い方について解説します。

有意差とは？

“仮説”と”実際の観察によって導き出された結果”の差が誤差では済まされないような、統計的に意味がある差を「有意差」と呼びます。

例えば、無作為に抽出した女性のグループと男性のグループで「ある商品Aを購入したことがある」という回答を収集したとします。
その回答が、

• 女性＝2,000回答
• 男性＝1,000回答

だった場合、明らかに女性の方が購入率が高く、ほとんどの場合「有意差がある」と言えそうではないでしょうか。

しかし、

• 女性＝1,003回答
• 男性＝1,000回答

といった場合はどうでしょうか？ たしかに女性のほうが男性よりも回答数は多いものの、1,000という数値に対して、3はほとんど同数であり「ある商品Aの購入率は、男性よりも女性のほうが高い」とは言えないでしょう。

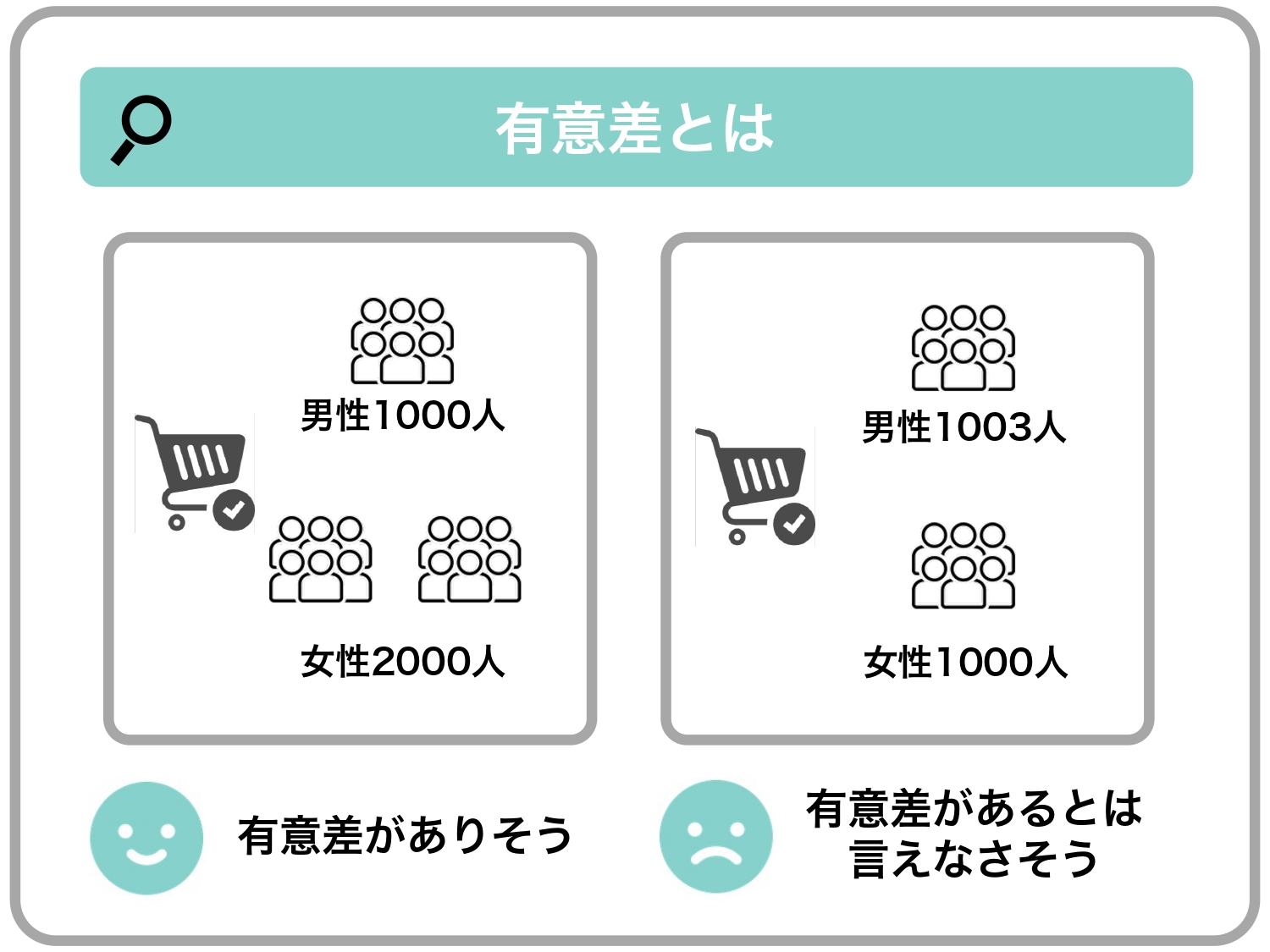
このように「1003と1000を比べたときにはほぼ同数なので、差は偶然によるものでありそうだ」というのは感覚的にも理解しやすいと思います。
では、

• 女性＝1050回答
• 男性＝1000回答

の場合はどうでしょうか？
さらに、

• 女性＝1100回答
• 男性＝1000回答

となった場合はどうでしょうか？

前例と比べ、「偶然ではないか」「いや、偶然ではないのではないか」、直感的にわからないことが多い差分ではないでしょうか。

このように「これは偶然の差？偶然ではない差？」と迷ってしまう際に、統計的に信頼がおける差なのか？を判定する検定を有意差検定と言います。 有意差検定を実施することで、実際の調査結果が意味のあるものなのかどうかを見極めることが可能です。

帰無仮説と対立仮説

有意差を考えるとき、帰無（きむ）仮説と対立仮説を知っておくとより理解が深まります。

▼帰無（きむ）仮説と対立仮説とは？

帰無仮説と対立仮説は互いに否定の関係にあります。 帰無仮説は、”ある仮説”が正しいのかを判断するために立てられる仮説です。 有意差の検定を行うときは、基本的に帰無仮説（＝「有意差がない」という仮説）が正しくないということを目指して行われます。

ここからは、具体例とともに考えましょう。

 

有意差検定の具体例：サイコロが歪んでいるのかどうかを調べる

サイコロを100回振ったとき、3の目が30回出たとします。 本来サイコロを100回振ったとき3の目が出る確率は1/6なので、せいぜい16~17回程度のはずです。 この差はたまたま偶然によるものだったのか、それともサイコロが歪んでいたのかを調べるにはどうしたら良いでしょうか？

まず、帰無仮説と対立仮説を設定します。 このとき、

と考えられます。

下の図の二項分布表を見てみると、サイコロを100回振ったときに3の目が30回出る確率は0.038%です（30回以上出る確率を見ても0.067%） ですので、100回振って同じ目が30回出たというのは、ほとんど偶然では起こり得ない「まれ」な現象であったということが分かります。

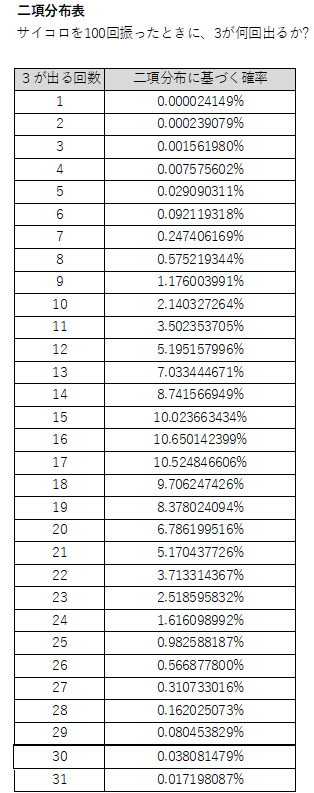
この結果は直感的には正しい感じがするのではないでしょうか？
ただし、厳密に言えば、この0.038%を「まれ」とみるかどうかは、そのときの「そもそもどのぐらいをもって希少とするか」という水準の設定によります。

0.038%は、10000回同じ実験を行ったときに3~4回は起こりうるかもしれないというぐらいの確率ですが、比較する水準をもし仮に0.01%（10000回に1回）としていたら、「水準よりは大きい」と言えてしまい、つまり「十分起こりうる」「あってもおかしくない」と考えられてしまいます。
このとき基準にする水準のことを有意水準といいます。有意水準は、数式に置き換えたときには「α」と表します。

有意水準は通常のアンケート調査では5%で設定されますが、逆に言えば「5%ぐらいの確率で、本当に偶然おこってしまうこともある」という水準です。調査の種類や精度によって有意水準は都度設定されます。
有意差検定はこのように有意水準によって「有意差がある」「有意差があるとはいえない」と結論が変わります。

さて、ここまで有意水準を仮に0.01%にしたときはサイコロの同じ目が100回中30回出ても偶然の可能性があるということを説明しましたが、 上の表では、「サイコロは歪んでいるとも歪んでいないとも言えない」と書いてあるだけで、「サイコロは歪んでいない」と表現していないことに注意が必要です。
有意差検定では、帰無仮説（＝「有意差がない」という仮説）のもとで、期待する結果（有意水準を上回る確率で事象が起こること）が生じなかったことを根拠として、帰無仮説を却下します。（論理学で言う背理法です）

このとき、帰無仮説が棄却されなかったからといって、帰無仮説＝正しいとなるわけではありません。帰無仮説が棄却されなかったというのは、ただ単に、結果が帰無仮説と矛盾しないということが分かっただけです。

◆帰無仮説と結論

	帰無仮説が正しい	対立仮説が正しい
帰無仮説を棄却しない	〇	誤り
帰無仮説を棄却する	誤り	〇

帰無仮説の棄却と結論の関係は上の図のようになっています。 このポイントは有意差検定を行ったときによく間違いやすいところなので、よく注意しておきましょう。

ビジネスで有意差が活用される場面

有意差は、このように仮説が正しかったか否かを知るのに有効です。そのため、ビジネスの場面でも活用されることがあります。

有意差の活用１．アンケート結果の分析

消費者の意見を聞くにはアンケートの実施が有効です。 しかし、アンケートの結果には偶然の数字の偏りが出ることがあります。

例えば、ある商品の売上を見込んで商品を入荷したのに、数日経っても実際には商品の売れ行きが良くなかったというとき、それだけで「この商品は売上が立たない商品だ」という結論に至ることはできません。

なぜなら、先ほどのアンケート同様、この数日間の売上だけがたまたま悪かった（＝誤差だった）という、ただの偶然の可能性があるためです。そこで、得られた売上数のデータを元に、他の商品や他店と比べても有意にこの商品が売上が悪いのか否かを検定します。

その結果、実際には「売上が悪い」と言うのは誤差の範疇であり、実際には他の商品と変わりなかった／明らかにこの商品の売上は有意に低かった、といった示唆を得て、正しい販売戦略をとることが出来るのです。

有意差の活用２．仮説の正誤を確かめる

商品の売れ行きについて分析するとき、有意差検定を用いることでより根拠のあるデータを求めることが出来ます。

例えば、ある調査から「女性は商品Aを購入する確率が高いのではないか」と仮説を立て実際に商品Aの女性向けマーケティングをしたら、思うように商品が売れなかったというパターンを見てみましょう。 このとき「よくわからないが仮説が間違っていたようだ」と諦めるのはやや早計です。

仮説は正しかったのか否かを判断するときにも有意差検定を使うことが出来ます。 というのもこの場合、調査を実施した女性のグループの中をさらに年代や住んでいる地域ごとのグループに分けて再調査をすると、当初の仮説に含まれなかった要素にも有意差があるという結果が出る場合があるのです。

調査実施時には単に「女性」と「男性」に分けて調査をし、「女性は商品Aを購入する確率が高い」という仮説が立てられたわけですが、「女性」の中にも年代や住んでいる場所などの細かい違いがあります。

それらの要素を加味せずターゲットをひとくくりに「女性」としてしまったせいで、本当にニーズのある女性に響くメッセージを発信できていなかったために思うような結果が得られなかった可能性が考えられます。

有意差検定を通して「女性は商品Aを購入する確率が高い」という仮説が不十分であることが明確になり、さらに調査を追加して行えば女性の中でもターゲットとすべきグループを特定できるようになるのです。 このように得られたデータに、他の要素が影響を与えているマーケティングにおける可能性を知る場合にも、有意差検定は有効です。

まとめ

本記事では有意差について解説しました。
有意差を用いデータ解釈をすることで、出た数値の差は誤差の範囲内であるかそうでないかを知ることができます。
有意差検定を行ってその結果を戦略を立てる際に役立てたい場合、データに影響を与える他の因子も考慮して結論を考えることが大切です。
調査を実施した際に集計した数値に何か他の要素が影響していないかを考えるとき、有意差検定を行い数値を一つの参考にしてみてください。