カイ二乗検定とは?検定手法を解説
2023年08月10日

集計結果に出た差が偶然なのかそうでないのかを確認しないまま分析してしまうと、仮説や分析を誤ってしまいます。その差が偶然の範囲内なのか、それとも何か意味(原因)があるために生じた差なのかを確認することが必要です。
そこで役立つ方法が、カイ二乗検定です。カイ二乗検定では、差が誤差や偶然によってたまたま生じる確率を確認できます。この記事では、カイ二乗検定の意味や検定を行う流れ、注意点を解説します。
カイ二乗検定は連続していないデータの集まりを検定する方法
カイ二乗検定は、カイ二乗分布※を利用する検定方法の総称です。カイは、ギリシャ文字のχ(カイ、エックスではない)を意味します。
※カイ二乗分布:「理論値からの食い違いの大きさ」について、確率的に表した分布
カイ二乗検定では、クロス集計表で表される、連続していないデータ(カテゴリカルデータ)の集まりについて検定を行います。カイ二乗検定でよく使われるのは「適合度検定」と「クロス集計表の表頭(ひょうとう)と表側(ひょうそく)の関係性を探る検定」の2種類です。
▼2つの検定の比較
| 適合度検定 | データの分布を描いたときに、理論的な分布と実際の分布が同じと言えるかを検定する。 |
|---|---|
| 独立性の検定 | 2つの変数の集計結果の数値の差に、関連があるかないかを検定する。 |
なお、カイ二乗検定と比較される検定には、例えば「t検定」があります。t検定は平均値の差に意味があるのかを検定するもので、カイ二乗検定は割合の差に意味があるのかを検定するものという違いがあります。
カイ二乗検定を行う際におさえておきたい統計用語
カイ二乗検定についてより深く理解するために、知っておきたい統計用語を2つ解説します。
自由度
自由度は、自由に決められるデータ数のことで、カイ二乗検定での判定に使用します。
【自由度の具体例】
男女10人ずつに「猫が好きか」を聞き取ったところ、以下の表に示すとおり男女合計で、「猫が好き」と「猫が好きではない」が10人ずつになりました。
▼「猫が好き」か男女で聞き取った結果
| 猫が好き | 猫が好きではない | 合計 | |
|---|---|---|---|
| 男性 | 10 | ||
| 女性 | 10 | ||
| 合計 | 10 | 10 | 20 |
ここで、男性の4人が「猫が好き」と答えたと仮定すると、残りの項目も以下のとおり自動で決定されます。この例では1つの値しか自由に設定できないため、自由度は「1」です。
▼「猫が好き」か男女で聞き取った結果(男性・「猫が好き」が4人)
| 猫が好き | 猫が好きではない | 合計 | |
|---|---|---|---|
| 男性 | 4 | 6 | 10 |
| 女性 | 6 | 4 | 10 |
| 合計 | 10 | 10 | 20 |
カイ二乗検定の自由度は以下で表現できます。
(m-1)×(n-1)
m:表の行(上記の例では男性・女性)、n:表の列(上記の例では猫が好き・猫が好きではない)
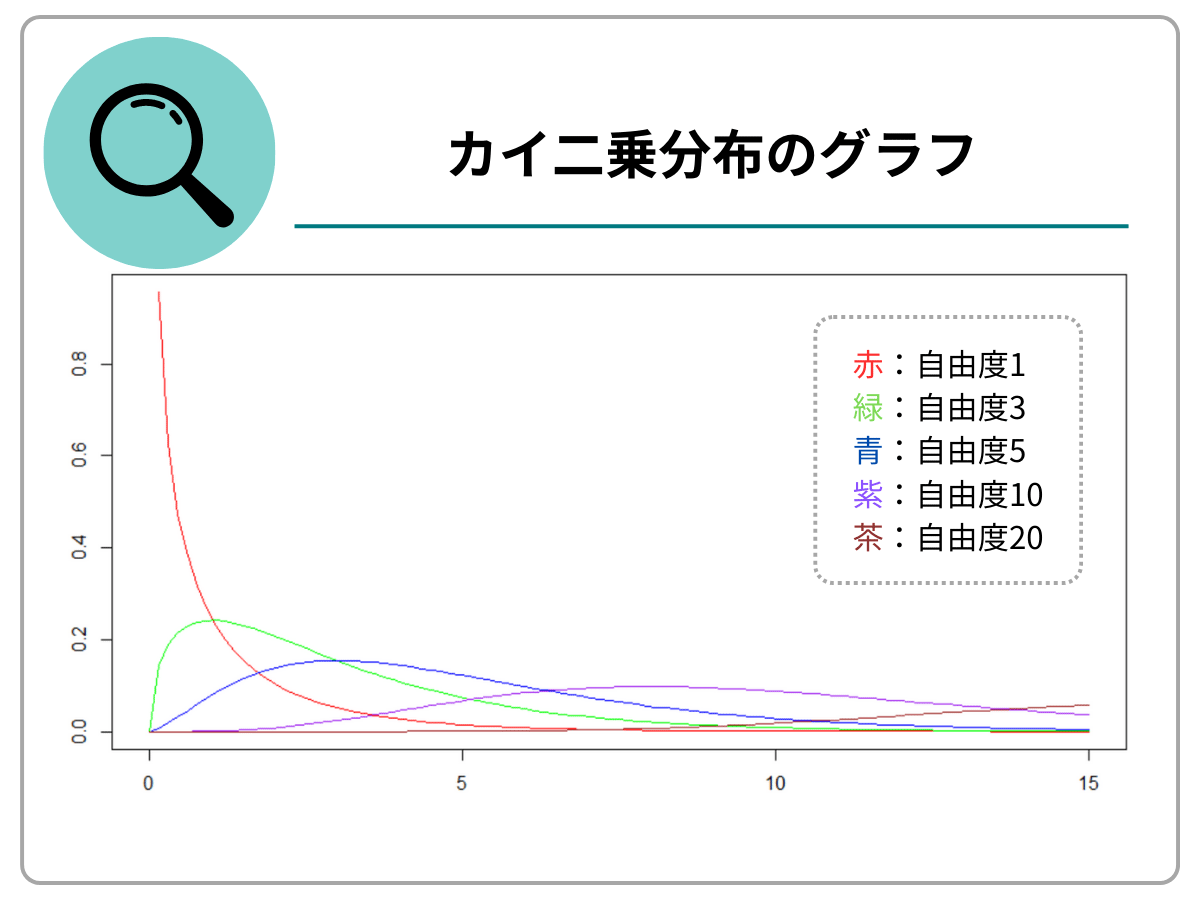
自由度が大きいほど、なだらかなグラフになり、正規曲線(左右対称な確率分布曲線)に近づいていきます。
帰無仮説、対立仮説
カイ二乗検定には、「適合度検定」と「独立性の検定」の2種類が存在します。両者とも、帰無仮説(差に意味はないとする仮説)と対立仮説(帰無仮説を棄却する仮説)の真偽を判定することで、検定を行います。
▼帰無仮説と対立仮説の比較
| 帰無仮説 | 有意差(誤差では済まないほどの差)がないとする仮説。通常は否定したい仮説を設定する。 |
|---|---|
| 対立仮説 | 有意差があるとする仮説。帰無仮説が間違っていると断定されたら(帰無仮説が棄却されたら)採用される。 |
帰無仮説が棄却されなかったからといって、帰無仮説が必ず正しいとは言えないませn。あくまでも、帰無仮説と矛盾しない程度に考えておくとよいです。
なお、帰無仮説と対立仮説、有意差については、「有意差とは?帰無仮説/対立仮説の考え方とビジネスでの活用を解説」に詳しく解説していますので参考にしてみてください。
【実践】カイ二乗検定で適合度検定を行うには?
適合度検定は、度数分布と理論分布とのズレが誤差の範囲か、そうでないのかを検定します。ここでは「A社の従業員100人の血液型の分布」を例に、検定の流れを見ていきましょう。
▼A社社員の血液型分布
| 血液型 | A型 | O型 | B型 | AB型 | 合計 |
|---|---|---|---|---|---|
| 度数 | 55 | 22 | 16 | 7 | 100 |
▼日本人の血液型の分布
| 血液型 | A型 | O型 | B型 | AB型 | 合計 |
|---|---|---|---|---|---|
| 度数 | 40% | 30% | 20% | 10% | 100% |
日本人では血液型の分布はおおよそ 上記のとおりとされていますが、A社社員の血液型の分布と、日本人の血液型の分布は同じと言えるでしょうか。適合度検定で判定してみましょう。
1.仮説を立てる
まずは、帰無仮説と対立仮説を立てましょう。今回の場合は、以下に設定します。
▼帰無仮説と対立仮説
| 帰無仮説H0 | 「調査した血液型分布は日本人の血液型分布と同じと言える」 |
|---|---|
| 対立仮説H1 | 「調査した血液型分布は日本人の血液型分布と同じとは言えない」 |
2.有意水準を設定する
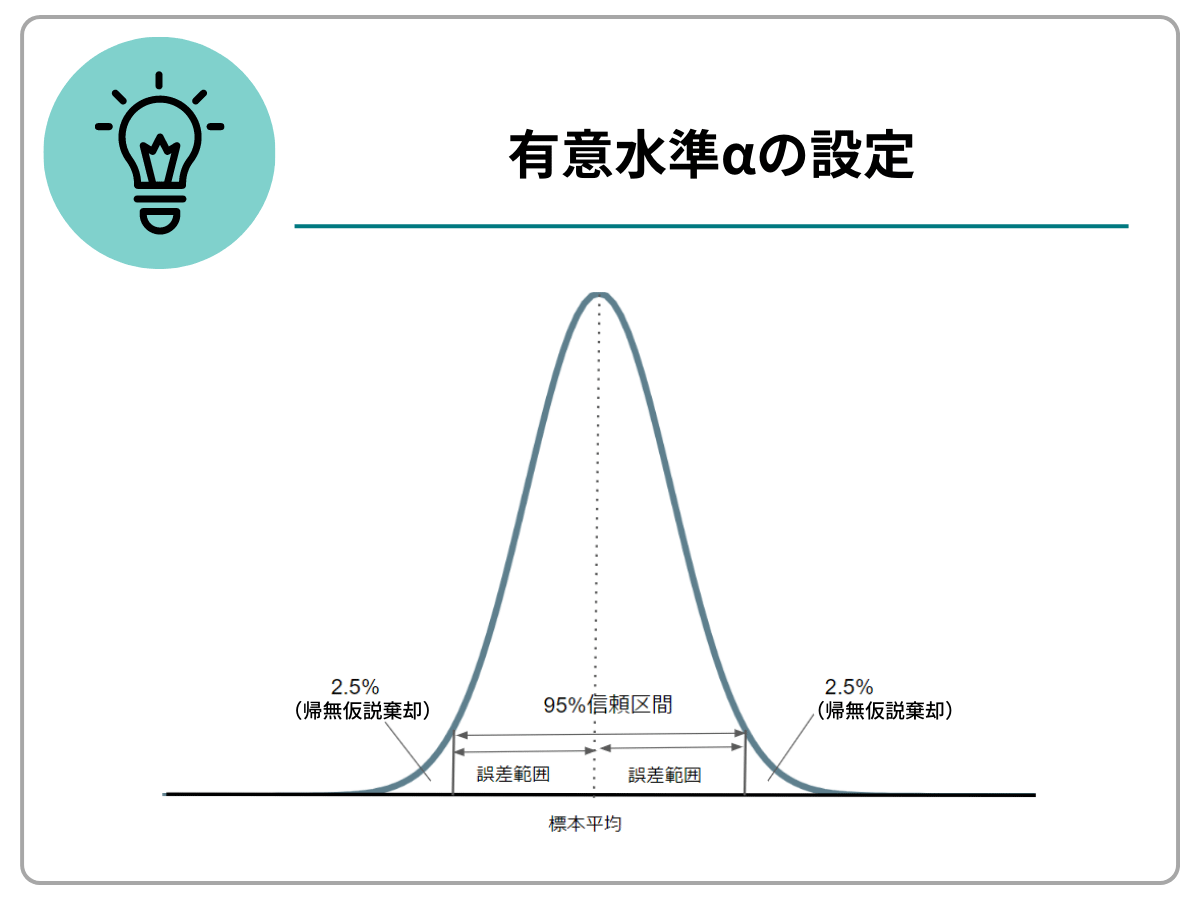
次に、有意水準αを設定します。
有意水準とは、検定において帰無仮説を設定した際にその帰無仮説を棄却する基準となる確率です。一般的には、有意水準には5%が採用されることが多いため、今回もα=5%=0.05を有意水準として採用します。
3.カイ二乗値を決定する
有意水準と比較するためのカイ二乗値を、2段階に分けて決定します。
1.まず、「理論値」からの「実測値」の差を二乗し、「理論値」で割ります。
▼血液型実測値と理論値の差
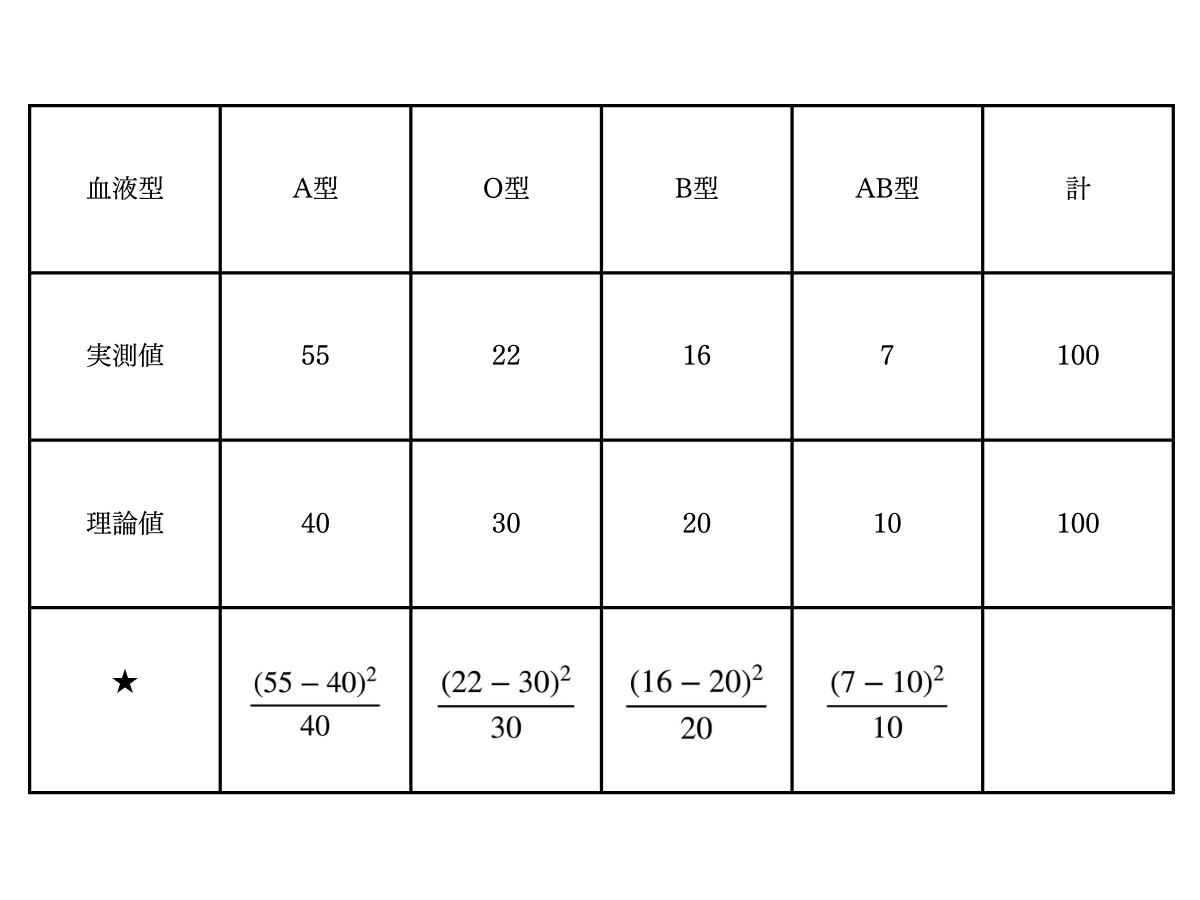
2.次に、①の★行の数値を合計します。
▼血液型実測値と理論値の差の合計
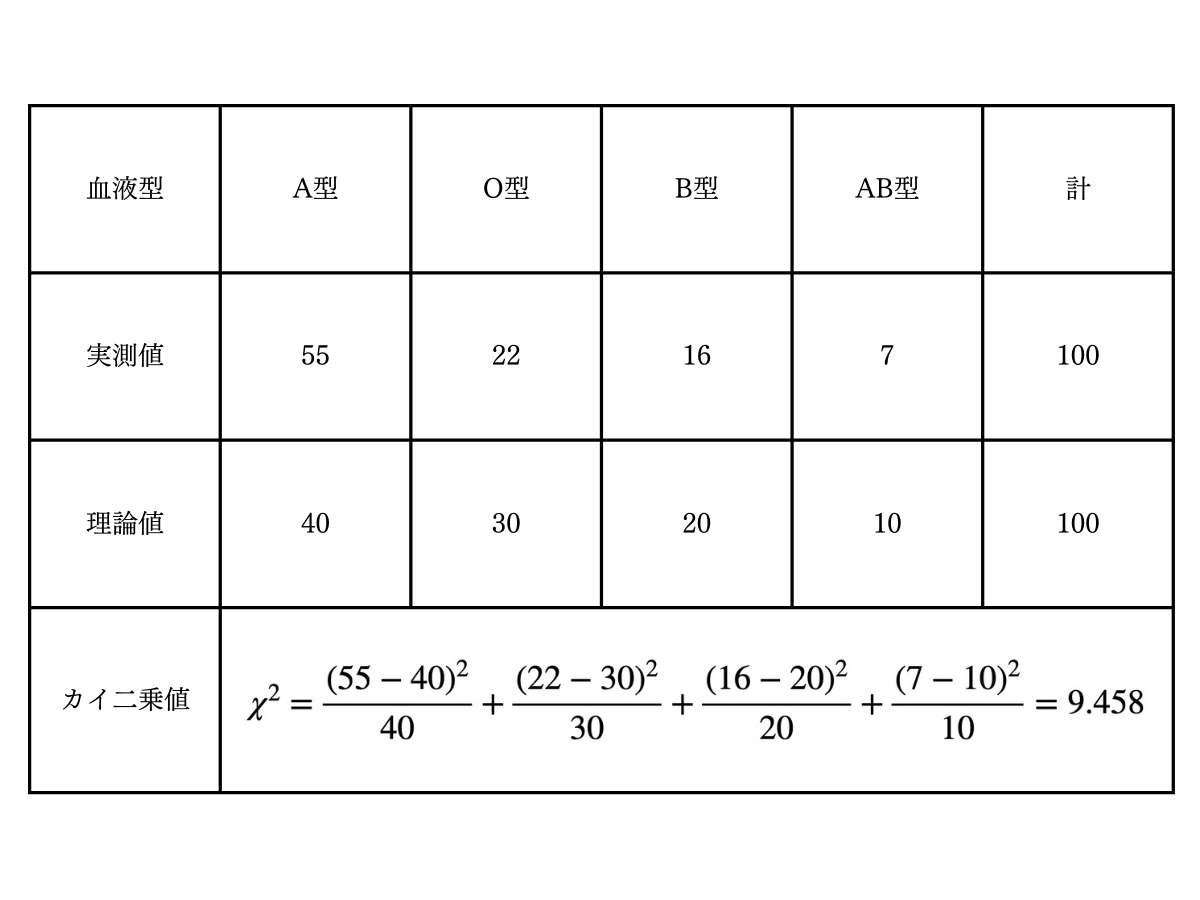
4.棄却ルールを決定する
棄却ルールとは、帰無仮説が間違っていると判断する基準のことです。今回の例では、自由度=4-1=3(血液型がA型、O型、B型、AB型の4種類であるため)で、有意水準はα=0.05です。
カイ二乗分布表(サイエンス社より引用)を見ると、自由度「3」、有意水準「0.05」のカイ二乗分布は、「7.81」だとわかります。カイ二乗値が「7.81」を上回れば、帰無仮説は棄却されます。
5.カイ二乗分布とカイ二乗値を比較して判定する
カイ二乗値(=9.458)がカイ二乗分布(=7.81)を上回っていますので、帰無仮説は棄却され、「A社の血液型分布と日本人の血液型分布は同じとは言えない」と判定できます。
【実践】カイ二乗検定で独立性の検定を行うには?
独立性の検定は、クロス集計表の2つのカテゴリの間に関連があるか検定することです。
男女100人ずつにアンケートを取り、猫が好きかどうかクロス集計表にまとめました。性別の違いと猫が好きかどうかに関連があるか、判定してみましょう。
▼男女で「猫が好き」かアンケートを取った結果
| 猫が好き | 猫が好きではない | 合計 | |
|---|---|---|---|
| 男性 | 50 | 50 | 100 |
| 女性 | 60 | 40 | 100 |
| 合計 | 115 | 85 | 200 |
1.仮説を立てる
まずは、帰無仮説と対立仮説を立てます。
▼帰無仮説と対立仮説
| 帰無仮説H0 | 「猫が好きかどうかと性別は独立である(関連がない)」 |
|---|---|
| 対立仮説H1 | 「猫が好きかどうかと性別は独立ではない(関連がある)」 |
2.有意水準を設定する
次に、有意水準αを設定します。今回もα=5%=0.05を有意水準として採用します。
3.理論値を計算する
カイ二乗検定では、実測値と理論値の差が、帰無仮説を棄却するほどの大きな差となっているかを判断します。
冒頭のアンケートを例に、理論値の求め方を解説します。
▼男女で「猫が好き」かアンケートを取った結果
| 猫が好き | 猫が好きではない | 合計 | |
|---|---|---|---|
| 男性 | A | B | A+B |
| 女性 | C | D | C+D |
| 合計 | A+C | B+D | A+B+C+D |
たとえば「男性」「猫が好き」と回答したセルの理論値は、以下の計算式で求めることができます。
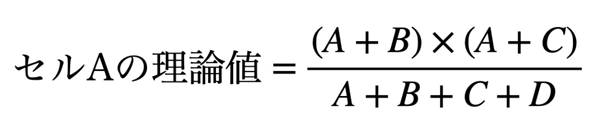
上の式に当てはめると、それぞれの理論値は以下になります。
▼男女の理論値
| 猫が好き | 猫が好きではない | 合計 | |
|---|---|---|---|
| 男性 | 55 | 45 | 100 |
| 女性 | 55 | 45 | 100 |
| 合計 | 110 | 90 | 200 |
4.カイ二乗値を決定する
「実測値」を「理論値」と比較するため、カイ二乗値を決定しましょう。「理論値」からの「実測値」の差を2乗し、「理論値」で割ります。
▼「理論値」からの「実測値」の差を2乗し、「理論値」で割った値

上記を合計すると、
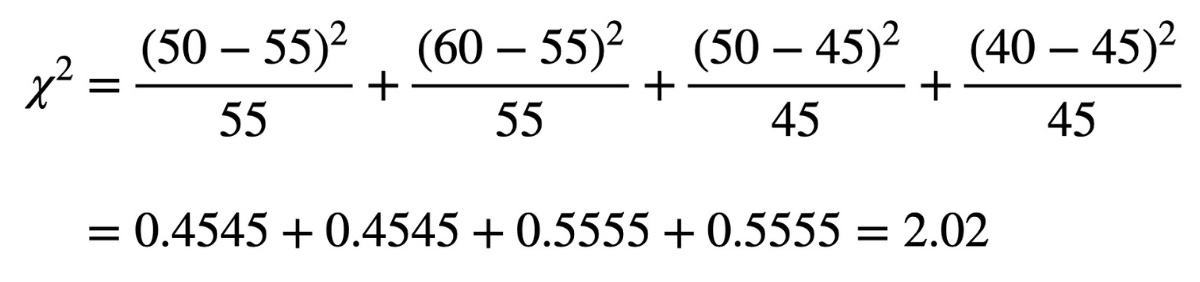
となりました。
5.棄却ルールを決定する
自由度は2ー1=1で、有意水準=0.05です。
カイ二乗分布表(サイエンス社より引用)を見ると、カイ二乗分布は「3.84」であることがわかります。カイ二乗値が「3.84」を上回れば、帰無仮説は棄却されます。
6.カイ二乗分布とカイ二乗値を比較して判定する
カイ二乗値(=2.02)がカイ二乗分布(=3.84)を下回っていますので、帰無仮説は棄却されず、「猫が好きかどうかと性別は独立である(関連がない)」と判定できます。
カイ二乗検定の注意点
ここまで、カイ二乗検定の意味や検定の流れについて解説してきましたが、カイ二乗検定を実施する際はいくつか注意すべき点が存在します。
まず、カイ二乗検定で用いるクロス集計表内のデータは、人数や頻度である必要があります。基本的に、%や比率などの数値は用いることができません。
理論値にも注意が必要です。分割表において、理論値が5未満となるセルが、全体の20%を上回る場合、カイ二乗値がずれる可能性が高いとされています。信頼できる結果を得るためにも、全体のうち理論値が5未満の値が20%を上回っていないか確認しましょう。
まとめ|カイ二乗検定で適合度や独立性を検定
カイ二乗検定は、カイ二乗分布を利用する検定方法の総称です。クロス集計表で表せる、連続していないデータ(カテゴリカルデータ)の集まりについて、適合度検定と独立性の検定を行うものです。
検定を行う際は、まず帰無仮説と対立仮説を立て、有意水準とカイ二乗値を決定します。その後、棄却ルールを決め、判定を行います。
思い込みやデータの見た目で判断せず、適合度検定や独立性の検定を活用して、データに現れる「差」を統計的にとらえましょう。
- 3分で読めるGMOリサーチ&AIのサービス
-
GMOリサーチ&AIでは、市場調査に役立つサービスを多数提供しています。
【サービス例】
- オンラインリサーチ
- 海外調査
- 消費者インサイト など
あなたの会社でも市場調査の結果を分析し、マーケティング活動に役立てませんか?
- GMOリサーチ&AIのサービスを知る
よくある質問
| Q1.カイ二乗検定の種類は? |
|---|
|
カイ二乗検定でよく使われるのは以下の2つの検定です。
詳しくは「カイ二乗検定は連続していないデータの集まりを検定する方法」の章をご覧ください。 |
| Q2.カイ二乗検定の注意点は? |
|
カイ二乗検定の注意点として、以下2つが挙げられます。
詳しくは「カイ二乗検定の注意点」の章をご覧ください。 |
- サービス概要を無料配布中「3分で読めるGMOリサーチ&AIのサービス」
-
GMOリサーチ&AIはお客様のマーケティング活動を支援しており、さまざまなサービスを提供しております。
- スピーディーにアンケートデータを収集するには
- お客様ご自身で好きな時にアンケートを実施する方法
- どこの誰にどれくらいリーチができるか
ぜひこの機会にお求めください。 - 資料請求する


