度数分布は、データを特定の範囲に分類し、それぞれの範囲にいくつのデータが該当するかまとめたもので、データの全体像をつかむために有効です。

度数分布は、例えば、以下のようなグラフで表現されます。

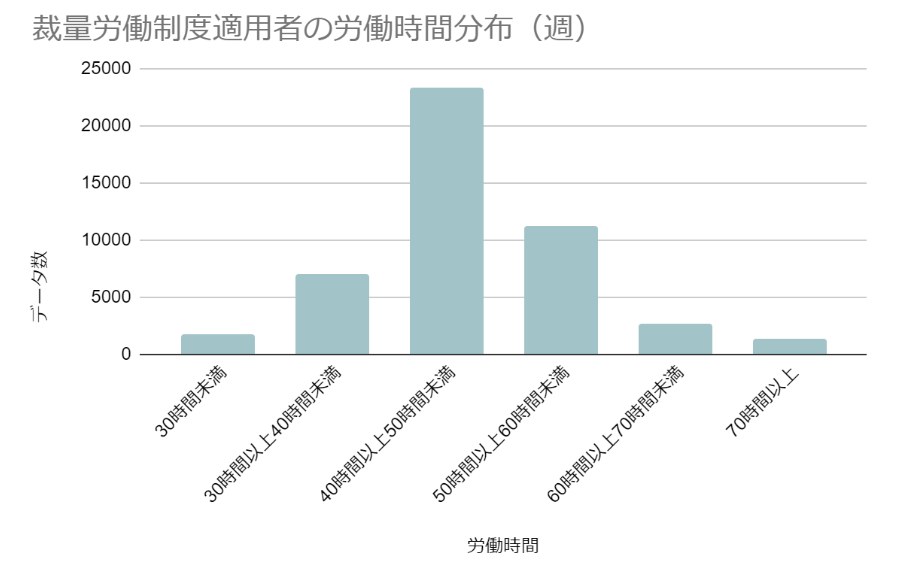
厚生労働省「裁量労働制実態調査の結果について（概要）」をもとに作成

この度数分布表から、半分近くの裁量労働制度適用者が週に40時間以上50時間未満で働いていることが一目で見て取れます。

また、度数分布から、平均値・中央値・最頻値を求めることもできます。

この記事では、度数分布の意味に加え、度数分布から平均値・中央値・最頻値を求める方法や、度数分布表をExcelやGoogleスプレッドシートなどの表計算ソフトで作成する方法を解説します。

度数分布とは「データ範囲ごとにデータ数をまとめたもの」

度数分布は、データの全体像をつかむために有効です。

例えば、世界の統計2022（総務省統計局）から抜粋した、アジア31カ国の男女平均寿命の一覧表を見てみましょう。

この一覧表には各国のデータが羅列されていますが、これだけでデータの特徴を推し量ることは困難です。

◆アジア31カ国の男女平均寿命一覧

国	男女平均寿命
日本	84
イスラエル	83
韓国	83
シンガポール	83
クウェート	81
トルコ	79
タイ	78
イラン	77
スリランカ	77
中国	77
アラブ首長国連邦	76
マレーシア	75
オマーン	74
カザフスタン	74
サウジアラビア	74
バングラデシュ	74
ブルネイ	74
ベトナム	74
ウズベキスタン	73
北朝鮮	73
シリア	73
イラク	72
インド	71
インドネシア	71
ネパール	71
カンボジア	70
フィリピン	70
ミャンマー	69
イエメン	67
パキスタン	66
アフガニスタン	63

 

 

しかし、以下のように度数分布表を作成することで、データの特徴を整理しやすくなります。

 

◆アジア31カ国の男女平均寿命の度数分布表

階級	階級値	度数	累積度数	相対度数	累積相対度数
60歳以上65歳未満	62.5	1	1	0.03	0.03
65歳以上70歳未満	67.5	3	4	0.1	0.13
70歳以上75歳未満	72.5	15	19	0.48	0.61
75歳以上80歳未満	77.5	7	26	0.23	0.84
80歳以上85歳未満	82.5	5	31	0.16	1
合計		31		1

 

 

 

 

 

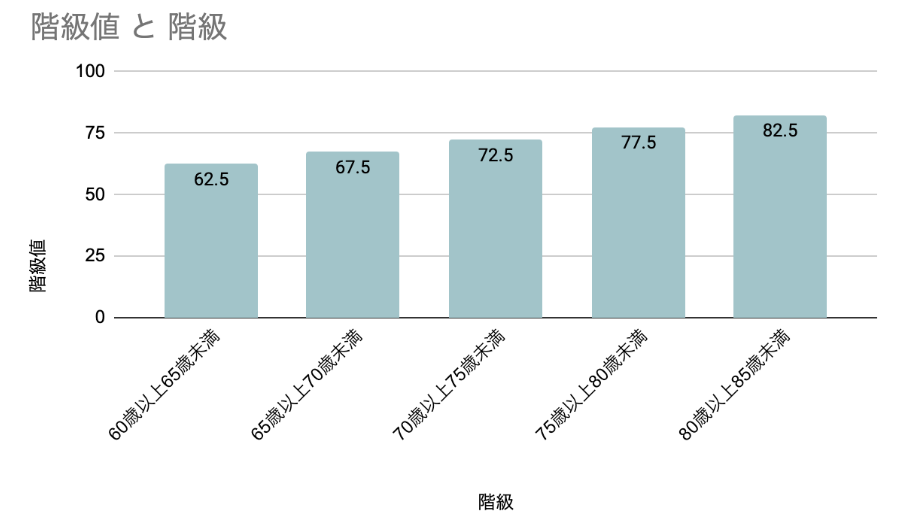
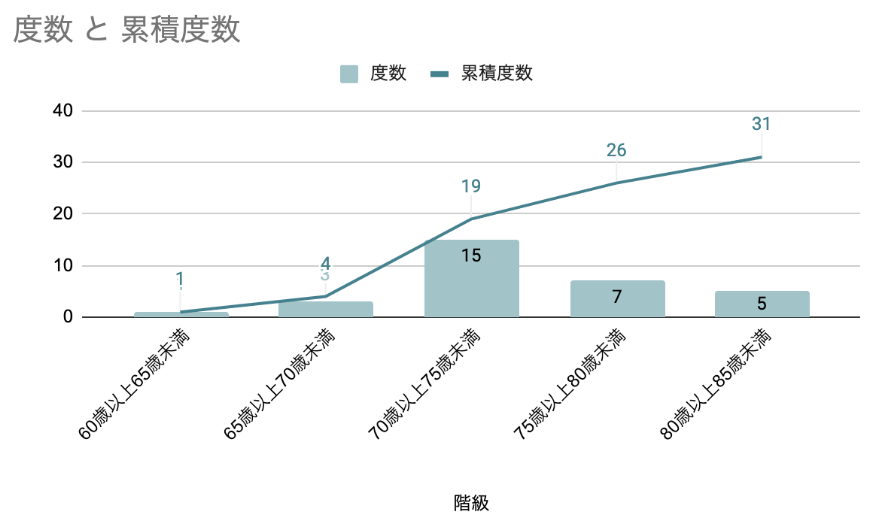
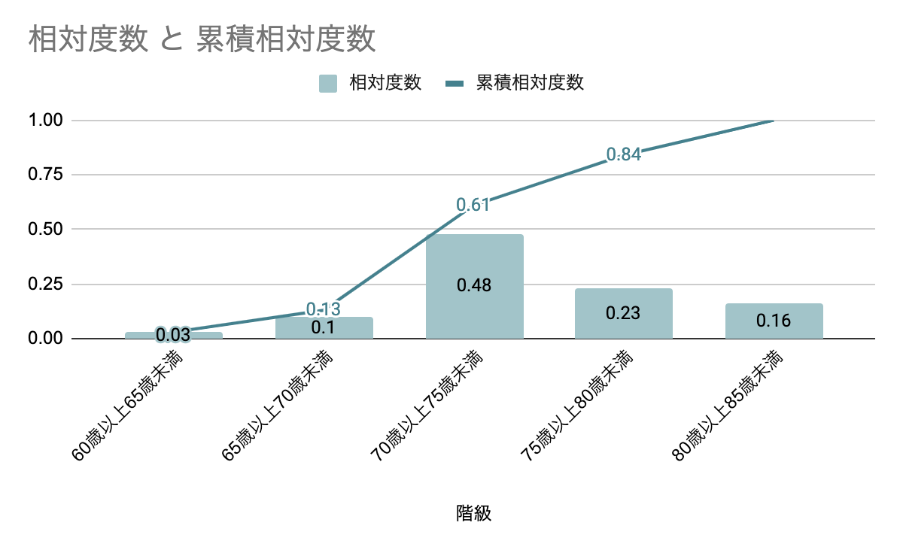
ここで、それぞれの表に示す値の意味を解説します。

階級｜度数を集計するための区間

階級は、度数を集計するための区間です。

上の例では、男女平均寿命が何歳以上何歳未満かで示しています。

階級値｜階級の真ん中の値

階級値は、その階級を代表する値のことで、階級の真ん中の値です。

上の例では、男女平均寿命が「70歳以上75歳未満」であれば、（70+75）÷2＝72.5が階級値になります。

度数｜各階級に含まれるデータ数

度数は、各階級に含まれるデータ数です。

上の例では、男女平均寿命が「80歳以上85歳未満」の国は、日本、イスラエル、韓国、シンガポール、クウェートの5カ国です。

そのため、「5」が「80歳以上85歳未満」の度数になります。

相対度数｜各階級の度数が全体に占める割合

相対度数は、各階級の度数が全体に占める割合です。%表記ではないことに、注意してください。

上の例では、男女平均寿命が「80歳以上85歳未満」の相対度数は、度数5カ国÷合計31カ国＝0.16です。

累積相対度数｜その階級までの相対度数の全ての和

累積相対度数は、その階級までの相対度数の全ての和（累積和）です。

「累積相対度数＝直前の累積相対度数＋今の相対度数」で計算され、最終的には累積相対度数は1になります。
例えば、「70歳以上75歳未満」であれば、直前の累積相対度数＝0.13、今の相対度数＝0.48なので、累積相対度数＝0.13＋0.48＝0.61となります。

度数分布から平均値・中央値・最頻値を求める方法

度数分布はデータ全体の特徴をつかむために有効ですが、他にもデータ全体の特徴をつかむために有効な概念が存在します。
その代表例が、平均値・中央値・最頻値の3つです。
これらは、3つとも度数分布から求められます。

ここでは、先ほど示したアジア31カ国の男女平均寿命の度数分布表を用いて、度数分布から平均値・中央値・最頻値を求める方法を解説します。

◆アジア31カ国の男女平均寿命の度数分布表

階級	階級値	度数	累積度数	相対度数	累積相対度数
60歳以上65歳未満	62.5	1	1	0.03	0.03
65歳以上70歳未満	67.5	3	4	0.1	0.13
70歳以上75歳未満	72.5	15	19	0.48	0.61
75歳以上80歳未満	77.5	7	26	0.23	0.84
80歳以上85歳未満	82.5	5	31	0.16	1
合計		31		1

 

◆度数分布表から求められた各値

平均値	約74.4歳
中央値	72.5歳
最頻値	72.5歳

平均値

平均値（Mean）は、データを単純に足し、その合計値をデータの数で割ったものです。度数分布表からは、具体的な個々のデータはわかりませんが、階級値から以下の値を平均値として採用します。

平均値＝Σ（階級値×度数）／度数の合計

さきほどのアジア31カ国の男女平均寿命の度数分布表にあてはめて考えると、以下の計算式から、平均値が約74.4歳であることがわかります。

◆計算式

中央値

中央値（Median、 メジアン、メディアン）は、データを昇順または降順に並べたときに、ちょうど真ん中にあたる値です。度数分布表では、ちょうど真ん中の値が属する階級の階級値が、中央値に該当します。

ただし、データの個数が奇数であればちょうど真ん中の値1つを選びますが、データの個数が偶数であれば、真ん中に最も近い値2つの平均値を使うことに注意してください。

男女平均寿命の例では、「70歳以上75歳未満」がちょうど真ん中なので、その階級値である「72.5」が中央値になります。

最頻値

最頻値（Mode、モード）は、最も多い頻度（度数）を示す値です。度数分布表では、度数が最も多い階級の階級値が、最頻値に該当します。

男女平均寿命の例では、「70歳以上75歳未満」の度数15が最も多い度数なので、その最頻値である72.5が最頻値です。

平均値・中央値・最頻値の違いについてより詳しく知りたい方は、下記コラムもあわせてご覧ください。

▼関連記事

【図解】平均値・中央値・最頻値の意味と使い分け｜リサーチコラム

度数分布表をExcel・Googleスプレッドシートで作成する方法

度数分布表は、Excel・Googleスプレッドシートなどの表計算ソフトで作成できます。キャプチャ画像を使って、Googleスプレッドシートで度数分布表を作る方法を、2つ解説します。

1．Frequency関数を活用する方法

Frequency関数は、条件に合致するセルの個数を数える関数です。

先ほど示したアジア31カ国の平均寿命のデータから、男女平均寿命が70歳以上の国をピックアップして、男女の平均寿命がそれぞれ以下の国がいくつあるか、Frequency関数で求めます。

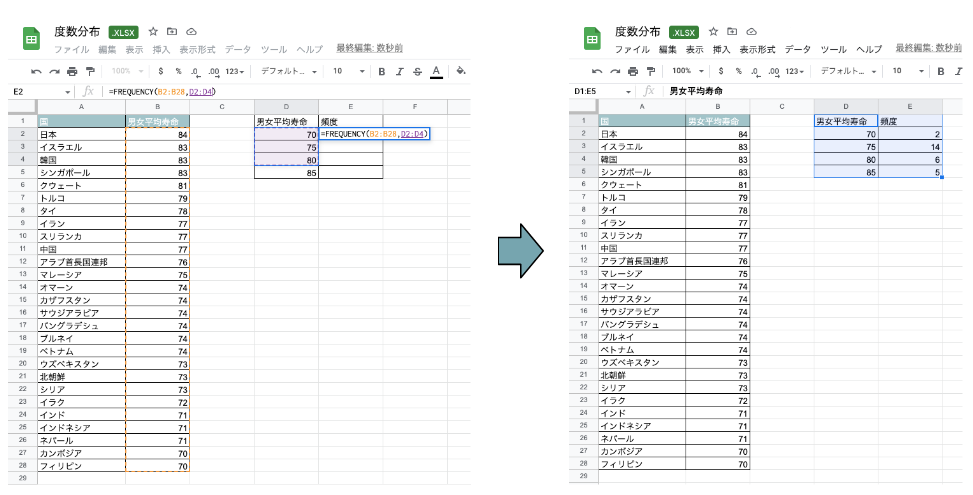
ここで、それぞれの列に記載している内容は、それぞれ以下のとおりです。

A列	国名
B列	男女平均寿命
D列	男女平均寿命が何歳以下か（例：D4では、75歳より大きく80歳以下）
E列	B列のうち、D列の条件に該当する国がいくつあるか示す

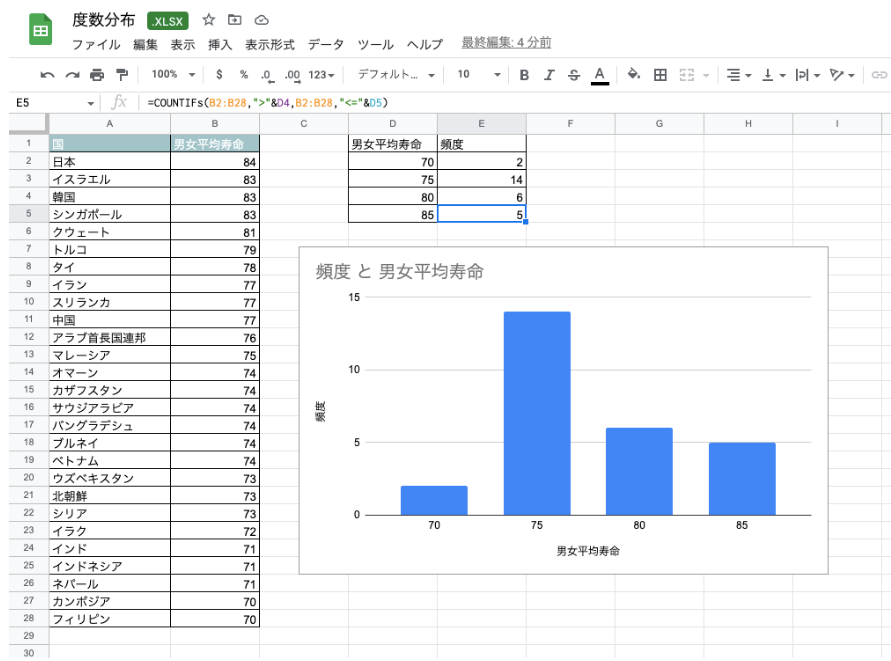
E2のセルに「=FREQUENCY(B2:B28,D2:D4)」を入力すると、度数分布表が出力されます。

このとき、E2には「D2:D4」と入力すれば、D5まで頻度が出力されることに注意してください。

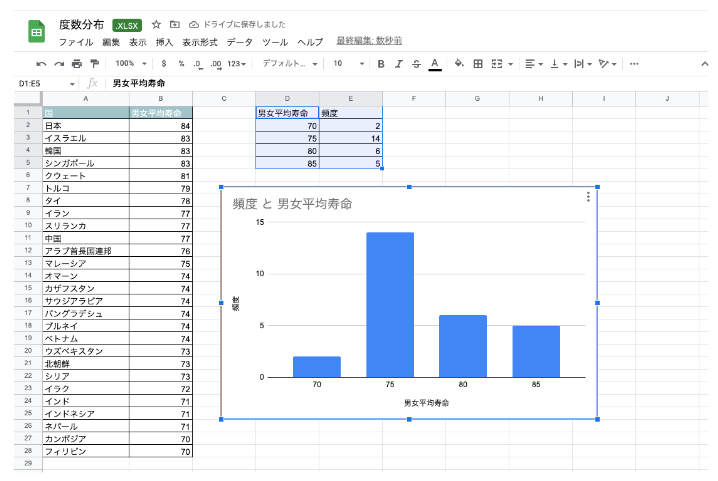
また、作成した度数分布表を選択し、メニューバーの「挿入」→「グラフ」で縦棒グラフを作成すれば、ヒストグラムを作れます。

 

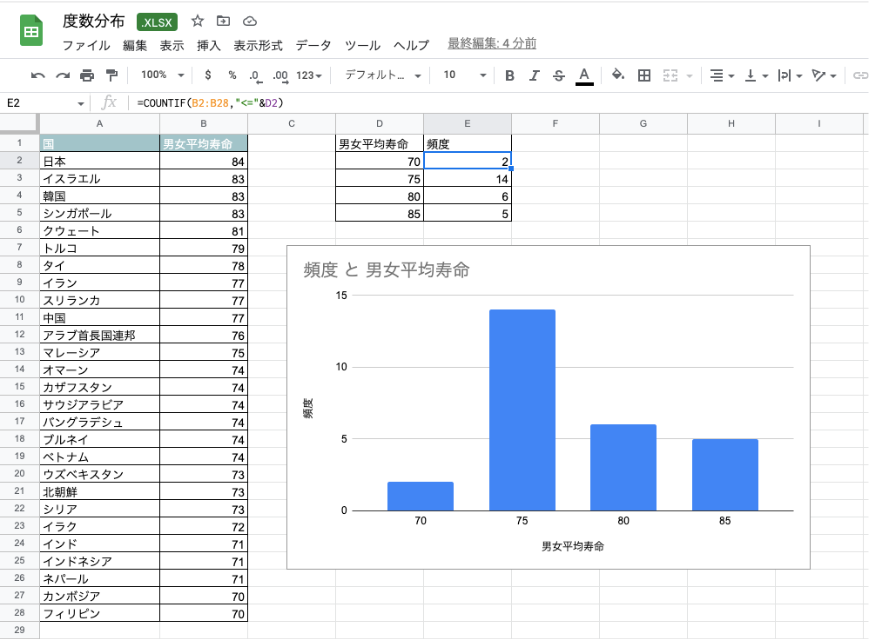
また、countif関数で条件に合致するセルの数を数えることも可能です。その場合、以下のどちらかで、それぞれの頻度を計算してください。

1. 条件が1つだけの場合は、「=COUNTIF(範囲,検索条件)」で計算
2. 条件が2つの場合は、「=COUNTIFS(範囲1,検索条件1,範囲2,検索条件2)」で計算

 

1．条件が1つだけの場合は、「=COUNTIF(範囲,検索条件)」で計算

以下の場合は、範囲が各国の男女平均寿命である「B2:B28」で、D2に示す「70」以下の条件に合致するセルの数を示しているのです。

2．条件が2つの場合は、「=COUNTIFS(範囲1,検索条件1,範囲2,検索条件2)」で計算

以下の場合は、これら2つの条件を同時に満たすセルの数を数えることで、男女平均寿命が80歳より長く、かつ85歳以下の国の数を数えられるのです。

• 範囲が「B2:B28」で、D4に示す「80」より平均寿命が長いという条件
• 範囲が「B2:B28」で、D5に示す「85」以下であるという条件

 

2．分析ツールを使う方法

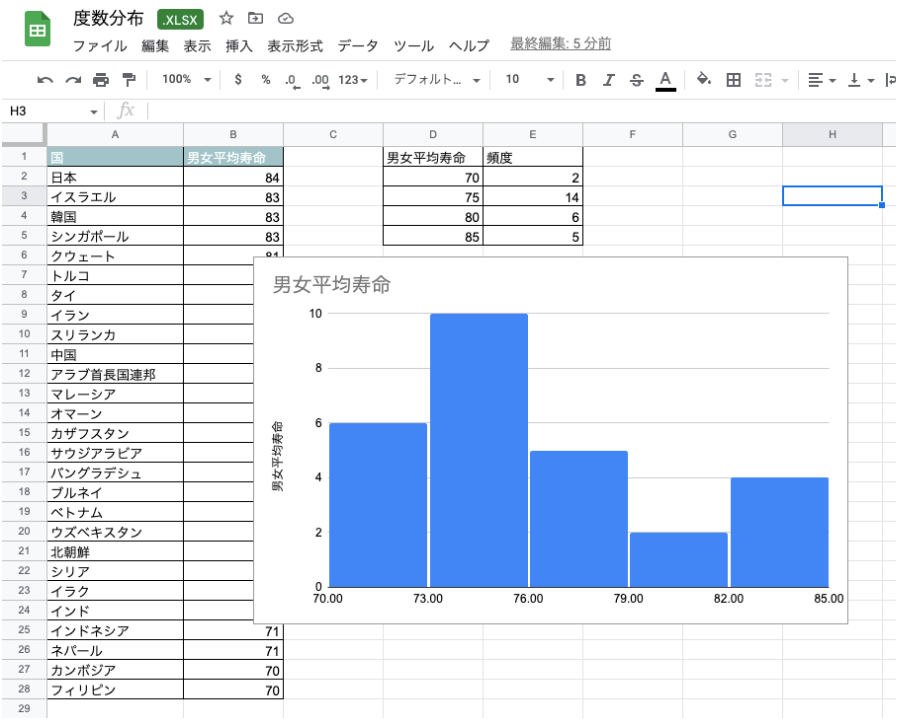
データを選択してからツールバーの「挿入」→「グラフ」でグラフを作り、そのグラフをヒストグラムにすることも可能です。

 

まとめ

度数分布は、データ数をデータ範囲ごとにまとめたもので、データの羅列だけではわからないデータの全体像をつかむために有効です。

また、度数分布から平均値・中央値・最頻値を求めると、さらにデータの特徴が明確になります。

度数分布表を作成する場合は、Frequency関数やグラフの作成機能を活用すると、簡単です。