移動平均とは?活用の目的とエクセルでの計算方法を解説
2024年01月05日
時系列データの分析は、将来の売り上げなどを予測する際に役立ちます。ただ、時系列データは、時間の経過以外のさまざまな要因に影響を受けるため、単純に折れ線グラフにするだけでは、データの傾向を把握しにくいことがよくあります。そこで有効な方法が、移動平均です。移動平均で時系列データを平滑化することで、よりデータ全体の傾向を把握しやすくなります。
この記事では、移動平均の意味を他の平均値との違いとともに解説し、併せてエクセルでの計算方法も解説します。
移動平均とは
移動平均とは、時系列データ(日々の売上金額や来客数など、時間経過によって変わっていくデータ)について、一定の範囲ごとの平均値をその範囲をずらしながら平均をとり、データを平滑化することです。
▼時系列データの例
- 自社サイトへのアクセス数
- 気温
- 株価 など
他の平均値とどこが違う?
移動平均は、一般的な平均(算術平均)を求める時と違い、時間の影響を受けることが特徴です。
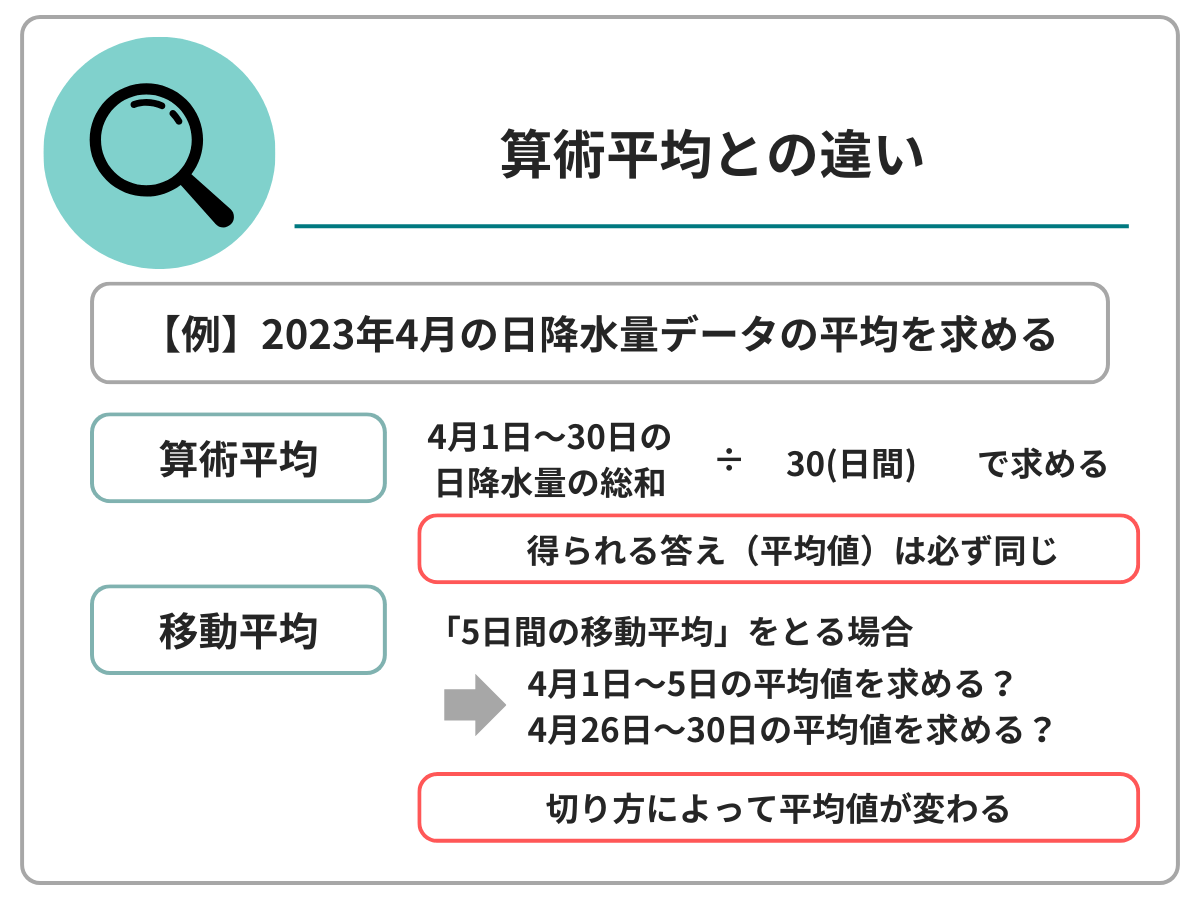
例えば、2023年4月1日〜4月30日までの日降水量データについて、平均値を取るとします。
算術平均では、2023年4月1日〜4月30日までのデータ全てを合計し、30日で割ることで平均値がわかります。計算対象の期間が固定のため、平均値が変わることはありません。
一方、移動平均では、例えば5日ごとの平均を計算する場合、4月3日の平均値は「4月1日~5日」のデータをもとに算出します。同様に、4月28日の平均値は「4月26日~30日」のデータに基づいて計算します。どちらの5日間も同じ気温の推移を辿るとは限りません。つまり、どの範囲を選択するかによって平均値が変わることになります。
移動平均を使うメリット
移動平均を使うメリットは、時系列データを分析する際に、データを平滑化することで傾向を把握しやすくなることです。Webサイトのアクセス数に関するデータを例に、移動平均を求めることでデータの見え方がどのように変わるのか確認してみます。
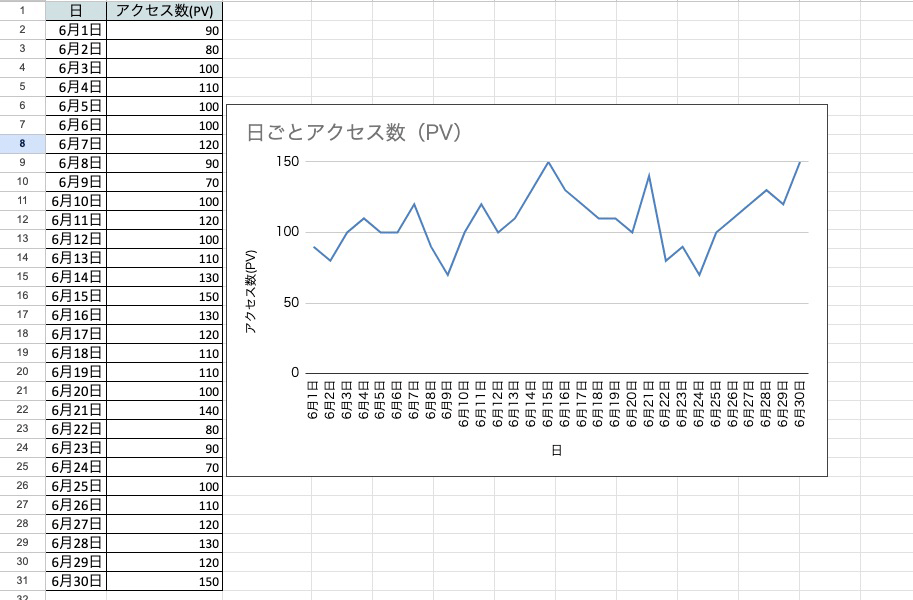
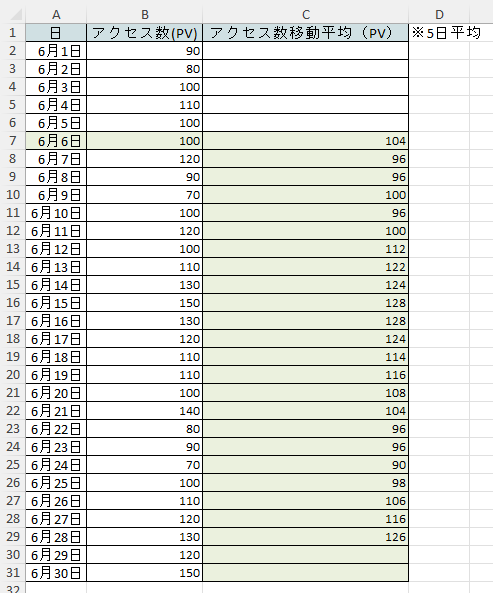
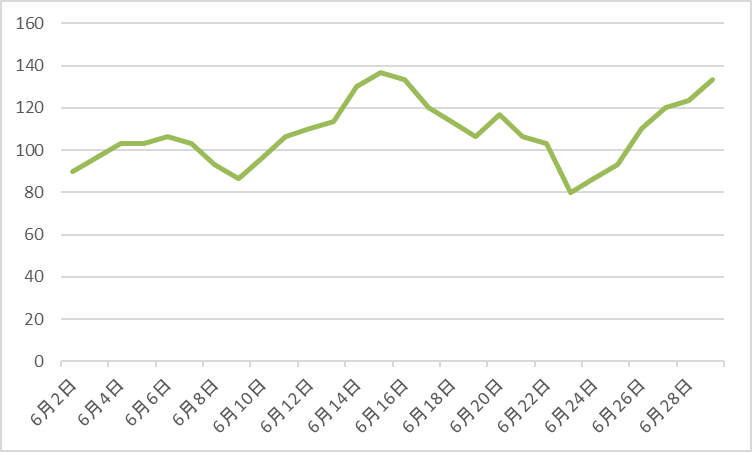
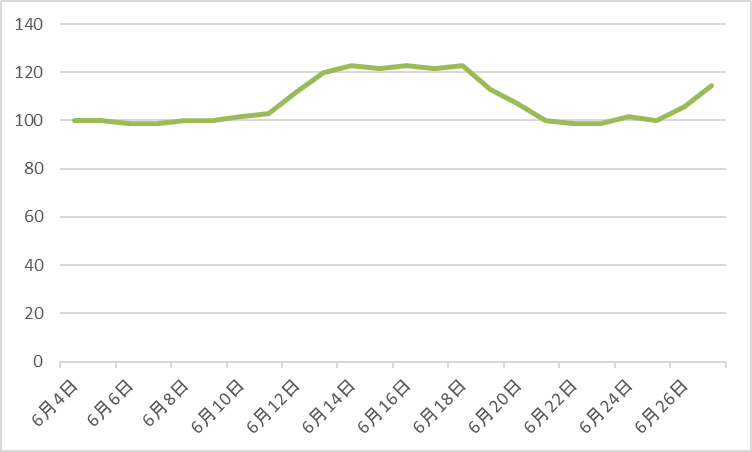
上の折れ線グラフ(青)は、2023年6月1日〜6月30日にかけて、Webサイトへのアクセス数を日ごとに記したものです。「この日はアクセス数が多かった・少なかった」など、1日ごとの動きはわかるものの、これだけではアクセス数が伸びているのか落ち込んでいるのか、大まかな傾向が把握しにくい状態です。
特に、今回例として挙げているアクセス数は、1日単位で増加・減少の変化が起きやすい数字です。多くのマーケターの方が、日ごとの推移よりも全体を把握したいと考えるのではないでしょうか。
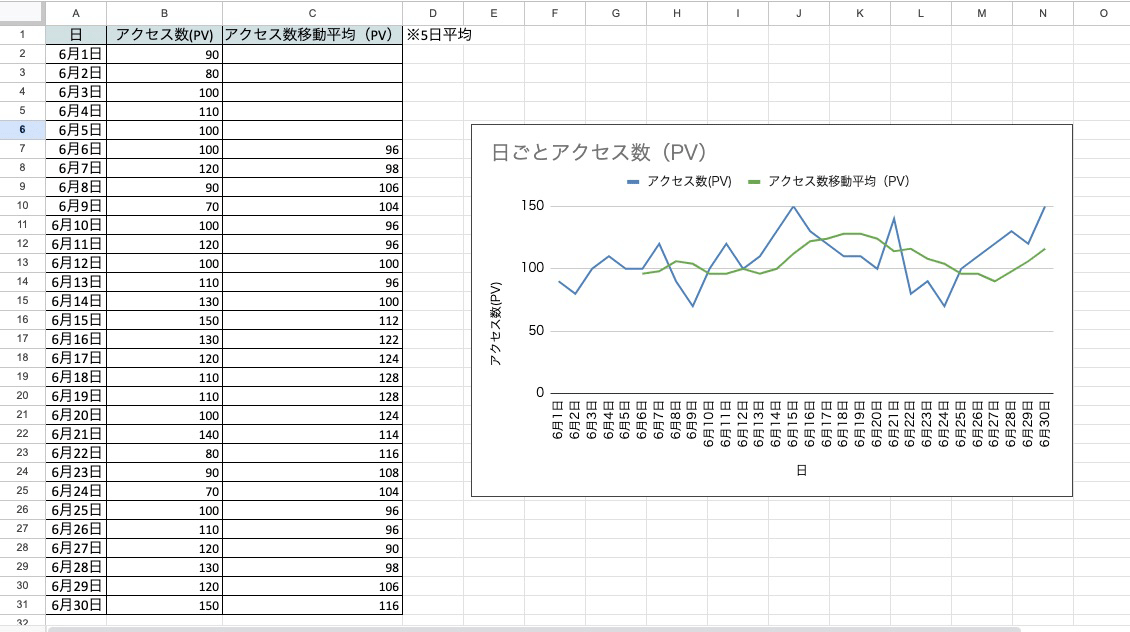
そこで役に立つのが、移動平均です。先ほどの折れ線グラフに、移動平均の推移(緑)も追記してみます。5日間ごとの移動平均をとっていますが、1日ごとのグラフよりも線がなだらかになり、「6月18日~20日ごろに向けて増加し、一度減少したが、再度月末に向かってアクセス数が伸びている」と、大まかな増減の傾向が見えやすくなります。
他にも、時系列データの特徴として、曜日や季節、トレンドの影響を受けたり、突発的な変化が見られることがあります。移動平均ではこれらの推移を平滑化するため、外部要因の影響を小さくしたうえで分析できるようになります。
時系列分析について詳しく知りたい方は、「時系列分析で将来を予測する|時系列データを意思決定に活かす方法」をご覧ください。
移動平均の求め方
移動平均は、まず区間を決め、次に計算式に当てはめることで求めることができます。本章では、先ほど例に使用した2023年6月1日〜6月30日のWebサイトへのアクセス数を用いて、具体的に解説します。

1.区間(n)を決める
まずは、前後いくつで区切るか、区間(n)を決めます。今回は日付ごとの推移を記録しているため、例えば「5日ごと」「7日ごと」など、日付を単位に区切ります。
▼例:6月6日の移動平均を求めたい
- 区間(n)=5日とした場合:前後2日で区切る(6月4日~6月8日)
- 区間(n)=7日とした場合:前後3日で区切る(6月3日~6月9日)
2.計算式に当てはめる
区間(n)を決めたら、次は移動平均を求める計算式に当てはめます。このとき、(n)が奇数か偶数かによって、計算方法が異なります。
2-1.区間が奇数の場合
区間が奇数の場合は、中心となる項から前後等間隔のデータを足し、区間(n)で割ることで求められます。
▼例1:区間(n)=5日で、6月6日の移動平均を求めたい
まずは、6月6日を中心とする5日間の時系列データを確認します。
| 日 | アクセス数(PV) |
|---|---|
| 6月4日 | 110 |
| 6月5日 | 100 |
| 6月6日 | 100 |
| 6月7日 | 120 |
| 6月8日 | 90 |
次に、このアクセス数をすべて足し、区間(n)=5で割ります。
(110 + 100 + 100 + 120 +90) ÷ 5 = 520 ÷ 5 = 104
つまり、区間(n)=5日の、6月6日の移動平均は「104(PV)」とわかります。
2-2.区間が偶数の場合
区間(n)が偶数の場合、中心となる項から前後等間隔の項を足していく点は奇数の場合と変わりません。しかし、区間を一つ大きくし両端の2つは、どちらも0.5倍してから足す必要があります。
▼例2:区間(n)=6日で、6月22日の移動平均を求めたい
まずは、基準となる日を中心に、区間(n)+1日の時系列データを確認します。
| 日 | アクセス数(PV) |
|---|---|
| 6月19日 | 110 |
| 6月20日 | 100 |
| 6月21日 | 140 |
| 6月22日 | 80 |
| 6月23日 | 90 |
| 6月24日 | 70 |
| 6月25日 | 100 |
次に、このアクセス数をすべて足し、区間(n)=6で割りますが、最初と最後の数字のみ0.5倍します。
(110 × 0.5 + 100 + 140 + 80 + 90 +70 + 100 × 0.5) ÷ 6 = 585 ÷ 6 = 97.5
つまり、区間(n)=6日の、6月22日の移動平均は「97.5(PV)」とわかります。
エクセルを使って移動平均を求める方法
移動平均はエクセルを使うことで簡単に求めることができます。関数を使用する方法と、アドイン機能を活用した方法の2種類を紹介します。
1.AVERAGE関数を使う
AVERAGE関数を使うことで、移動平均を求めることができます。前章同様、2023年6月1日~6月30日のWebサイトアクセス数を例に、計算してみます。
▼例3:区間(n)=5日で、6月6日の移動平均を求めたい
まずは、使用する時系列データを日付順に入力します。
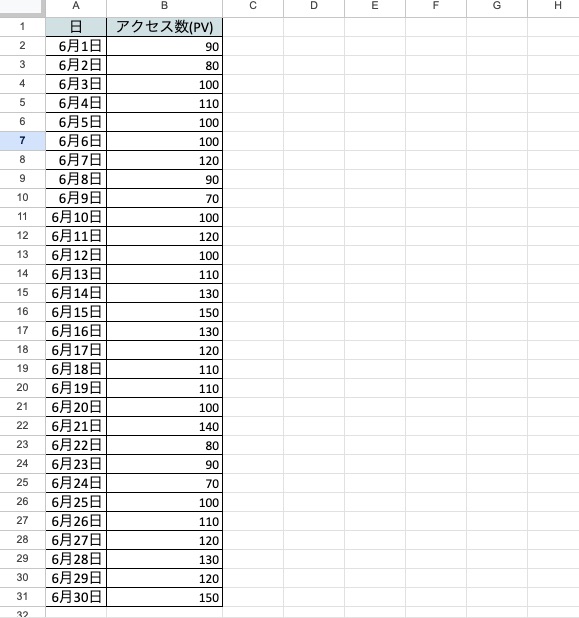
次に、6月6日を中心に5日間となるように、AVERAGE関数を入力します。
▼入力する関数
=AVERAGE(B5:B9)
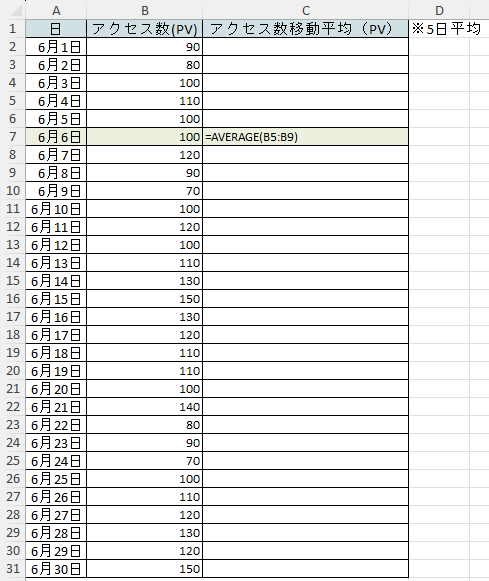
6月30日までの移動平均を求めたい場合は、関数を入れたセルから下までドラッグしていくことで、以下のセルにも計算式が反映されます。今回は区間(n)=5日のため、前後5日間のデータがわかる6月28日までドラッグしました。
6月6日〜6月30日までの移動平均をグラフにしたい場合は、データ範囲を選択し、「挿入」タブから「折れ線グラフ」を選択することで作成できます。
2.アドインを使う
アドインを使って、移動平均を求めることもできます。
アドインを使用したことがない場合はまず登録から行います。登録手順は簡単で、エクセルの「ファイル」タブを開き、左下にある「オプション」から「アドイン」を選びます。中央下部にある「設定」をクリックしたら以下画面が表示されるので、「分析ツール」にチェックを入れてください。
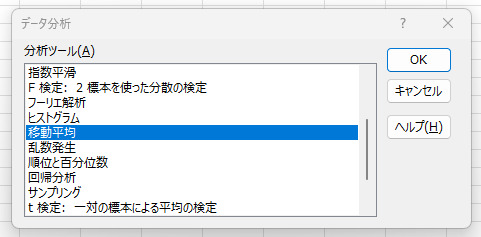
アドインを使う準備ができたら、「データ」タブから「データ分析」をクリックし、表示される分析ツールから「移動平均」を選びます。
「入力範囲」「区間」「出力先」をそれぞれ入力し、OKをクリックします。
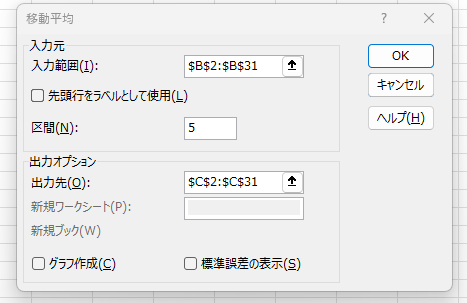
これで、簡単に移動平均を算出できます。
移動平均を求める際の注意点
移動平均を求める際に留意しておきたい点が1つあります。それは、平均する区間を広げるほど、細かな変化に気づきにくくなってしまう場合があることです。
例えば、同一データで区間(n)=3日とした移動平均と、(n)=7日の移動平均を比較します。
▼3日平均
▼7日平均
区間(n)=7日のグラフのほうが、(n)=3日のグラフよりも、折れ線の変化が滑らかになっていることがわかります。時系列データの特徴を大まかに掴むのに最適な移動平均ですが、今回のデータで7日平均としてしまうと、ほぼ横ばいのグラフとなってしまい、推移が逆に把握しにくくなってしまいます。
区間(n)を決める際は、変化を把握できる適切な間隔で取るようにすることが大切です。
まとめ|移動平均を活用し、データ全体の傾向を掴む
移動平均は、時系列データを使って、一定の範囲ごとの平均値を、範囲をずらしながら平均を計算することでデータを平滑化するものです。算術平均と違い、平均値を取る範囲によって、値が異なるのが特徴です。
移動平均を用いることで、曜日や季節、トレンドなど外部要因の影響を受けて傾向がわかりにくい時系列データのグラフを平滑化して、トレンドを把握しやすくします。エクセルでも容易に計算できるので、将来の売り上げ予測などを行う際に効果的な手法です。
- 3分で読めるGMOリサーチ&AIのサービス
-
GMOリサーチ&AIでは、マーケティング活動に役立つデータを取得するため、さまざまなサービスを提供しています。
- ネットリサーチ
- 海外調査
- 消費者インサイト など
少しでも興味がある方は、お気軽にご相談ください。
- 資料ダウンロード
よくある質問
| Q1.移動平均と算術平均の違いは? |
|---|
|
大きな違いは、時間の影響を受けることです。 算術平均では、単純にデータの合計をデータ数でわるだけなので、同じデータを同じ期間で算術平均すれば答えは1つです。一方移動平均では、平均値を取る範囲によって、計算結果が変わってきます。 詳しくは、「他の平均値とどこが違う?」の節をご覧ください。 |
| Q2.移動平均をエクセルで計算する方法は? |
|
移動平均をエクセルで計算する方法は、以下の2つに大別されます。
それぞれを活用した計算手順については、「エクセルを使って移動平均を求める方法」の章をご覧ください。 |
- サービス概要を無料配布中「3分で読めるGMOリサーチ&AIのサービス」
-
GMOリサーチ&AIはお客様のマーケティング活動を支援しており、さまざまなサービスを提供しております。
- スピーディーにアンケートデータを収集するには
- お客様ご自身で好きな時にアンケートを実施する方法
- どこの誰にどれくらいリーチができるか
ぜひこの機会にお求めください。 - 資料請求する


