時系列分析とは、時間経過に伴って変化するデータを分析することです。例えば、毎日の売上金額や、来客数、株価などのデータが時系列分析の対象にあたります。

これらのデータがどのような変動要因から影響を受けているのか分析し、モデルを適用して将来のデータ数値の予測まで行います。時系列分析は、勘や経験に頼らず、データドリブンな意思決定を行うために有効です。

この記事では、時系列分析の意味や注意点、代表的なモデルまで図解でわかりやすく解説します。

時系列分析｜時間経過に伴って変化するデータの分析

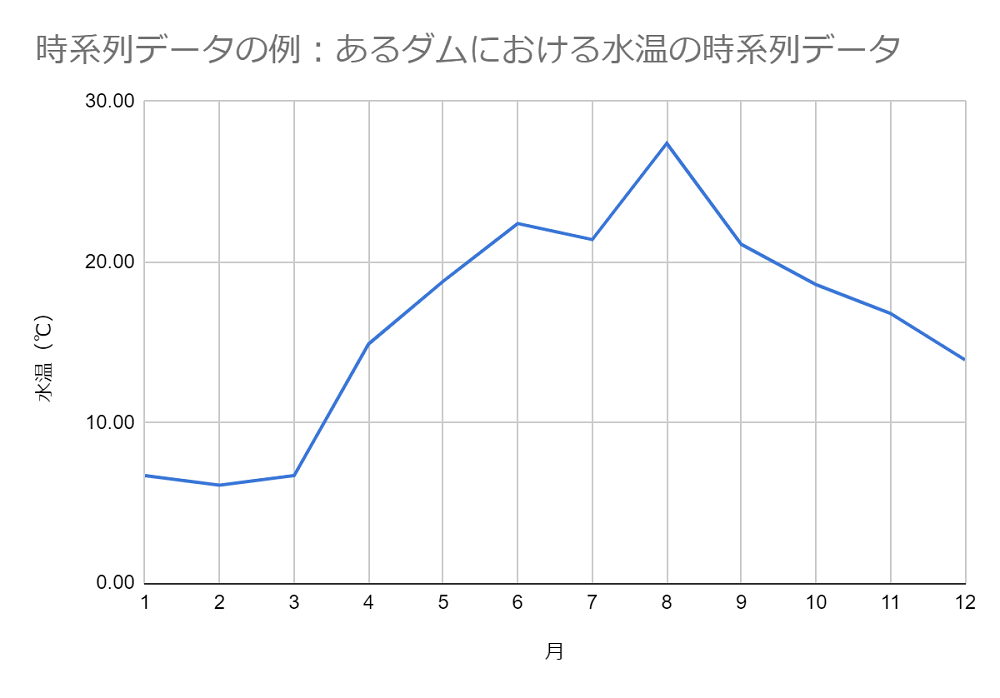
時系列分析とは、「時系列データ」を分析することです。

時系列データとは、厳密に定義すれば「時間経過に伴って変化するデータを、特定の時間間隔（年・月・日など）で観測した結果の集まり」です。

時系列データの対義語は、ある一定時点を断面的に切り取った「横断面データ（クロスセクションデータ）」です。例えば、あるサービスの某日時点での利用者割合や、ある年の売上の内訳などをイメージすると良いでしょう。

◆横断面データの例

時系列データを扱う場合、横軸に観測時間、縦軸に観測対象のデータの値をとり、折れ線グラフの形で視覚化することが一般的です。

ビジネスにおいてデータと時間的概念を紐づけて分析することで、日々移り変わる数値の分析や将来の予測を行うことが可能です。例えば、毎日の売上金額や、来客数、生産販売量、株価、広告クリック数などのイベント数、離職者数などです。

ただし、データの時間的特性を考慮するためには、いくつか扱いに注意が必要です。なぜなら、ある対象やその属性が、連続した時間上にあり、変化しているという特性によって、明示的な関数を規定することが困難なためです。

そのため、時系列データを扱う場合には、事前にデータに一定の処理をおこなったり、変動のパターンを想定したりすることで、できる限りデータを扱いやすいようにします。

時系列データを適切に処理し、適したモデルを適用することで、将来のデータの変動を予想することができます。

重回帰分析との使い分け｜時系列データなら時系列分析

なお、データから結果を予測するときに、重回帰分析を用いるのではないかと考える方がいるかもしれません。重回帰分析とは、いくつかの変数との相関関係を数式化してある結果を予測する統計手法です。

◆重回帰分析の例

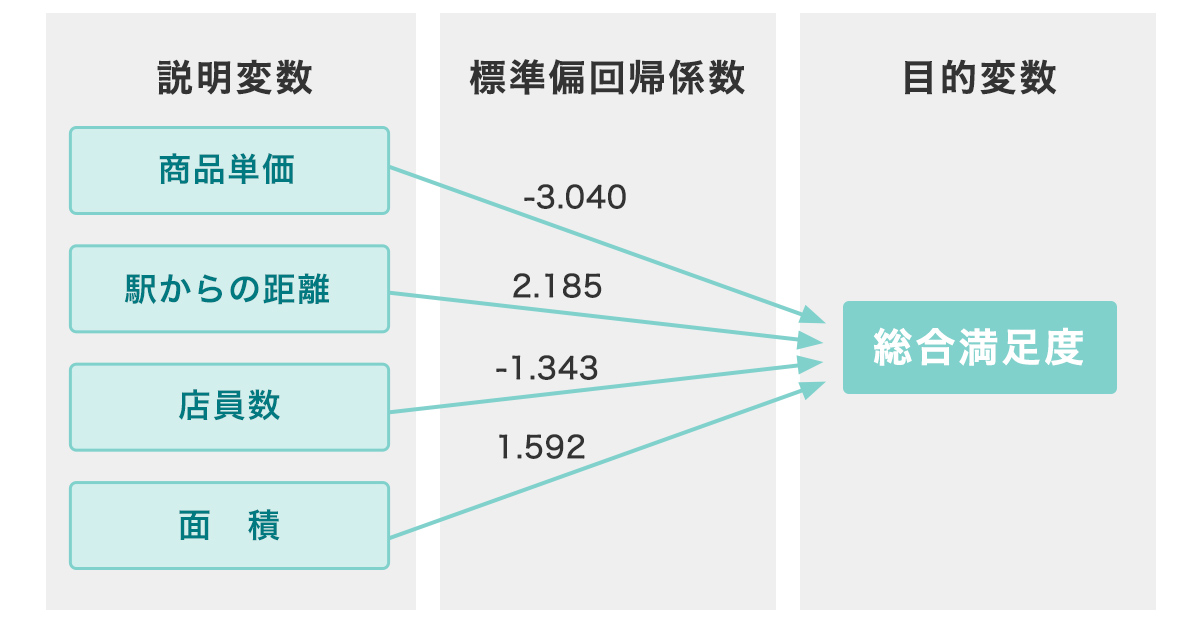
重回帰分析は、時間的概念を取り除いたテーブルデータの取り扱いには向いていますが、時系列データには向いておらず、精度が低下します。時系列データではデータが規則的に変動し、影響を受けてしまうためです。

時系列データをあつかう分析においては、各変動要因を考慮できる時系列分析が適しています。

▼関連記事

重回帰分析とは？ビジネスでの活用シーンや方法・注意点を解説 | リサーチコラム

時系列データの主な処理方法

時系列分析においては、時系列データが時間的に連続して変化しているという特性を考慮するために、データを特殊に変換処理することがあります。

◆時系列データの処理方法

原系列（げんけいれつ）	・処理される前の、単に時系列ごとに並べられたデータ 例）x1、x2、x3、x4、x5
差分系列	・1時点前のデータとの差をとった時系列データ ・経時変化を求めるときに便利 例）y1=x2-x1、y2=x3-x2、y3=x4-x3、y4=x5-x4
対数系列	・対数変換された時系列データ ・データのばらつきが大きいときに有効 例）log(x1)、log(x2)、log(x3)、log(x4)、log(x5)
対数差分系列	・対数系列において、差分を取った時系列データ ・対数データの経時変化を求めるときに便利 例）log(y1)=log(x2)-log(x1)、log(y2)=log(x3)-log(x2)、log(y3)=log(x4)-log(x3)、log(y4)=log(x5)-log(x4)
季節調整系列	・季節変動の影響を調整したデータ ・季節による影響をなくすことで、より純粋に長期変動を分析できる 例）log(y1)=log(x2)-log(x1)、log(y2)=log(x3)-log(x2)、log(y3)=log(x4)-log(x3)、log(y4)=log(x5)-log(x4)

時系列データに影響する3つの要因

時系列分析で扱う時系列データは、大きく3つの変動要因で構成されます。

１．長期変動

２．季節変動

３．不規則変動

この3つの変動要因がどのように組み合わさっているのか、時系列データを分解し、それぞれの要因を分析します。

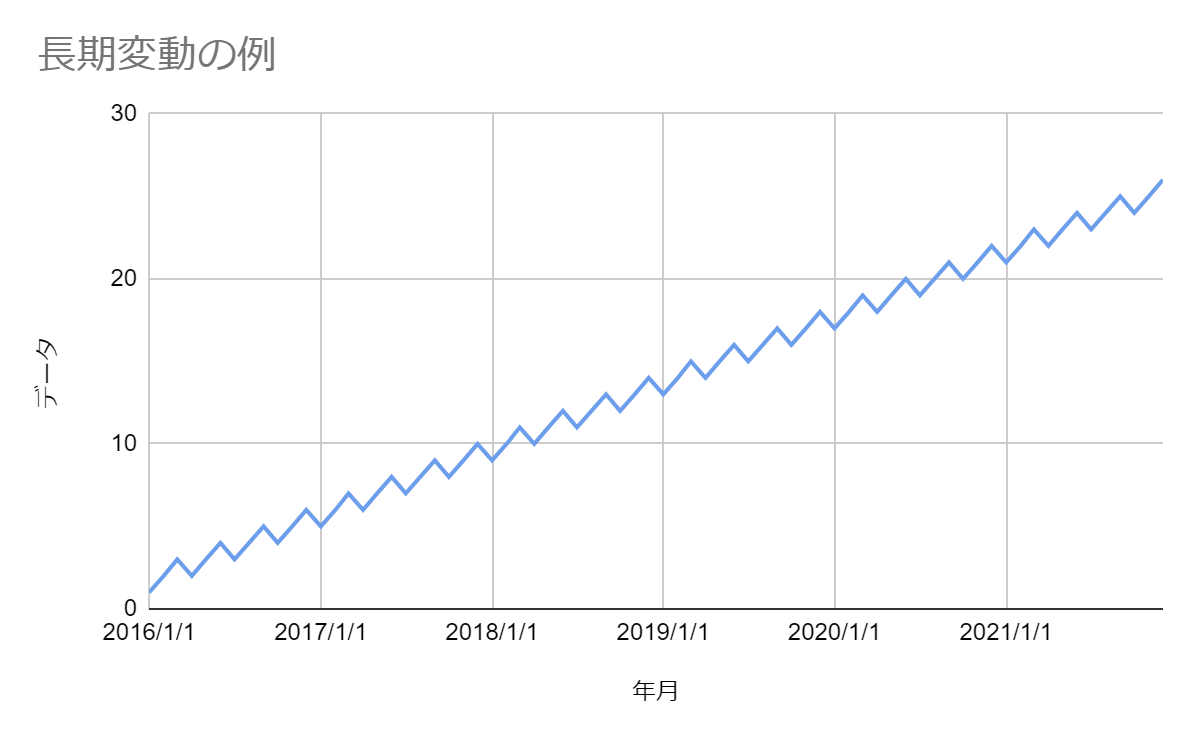
長期変動

長期変動は、時系列変動の長期的な傾向です。

時間の経過とともに、全体的に増加（もしくは減少）する傾向が見られる場合は、その傾向を長期変動と呼びます。必ずしも直線であるとは限らず、景気循環などの2年以上の長い周期も含みます。

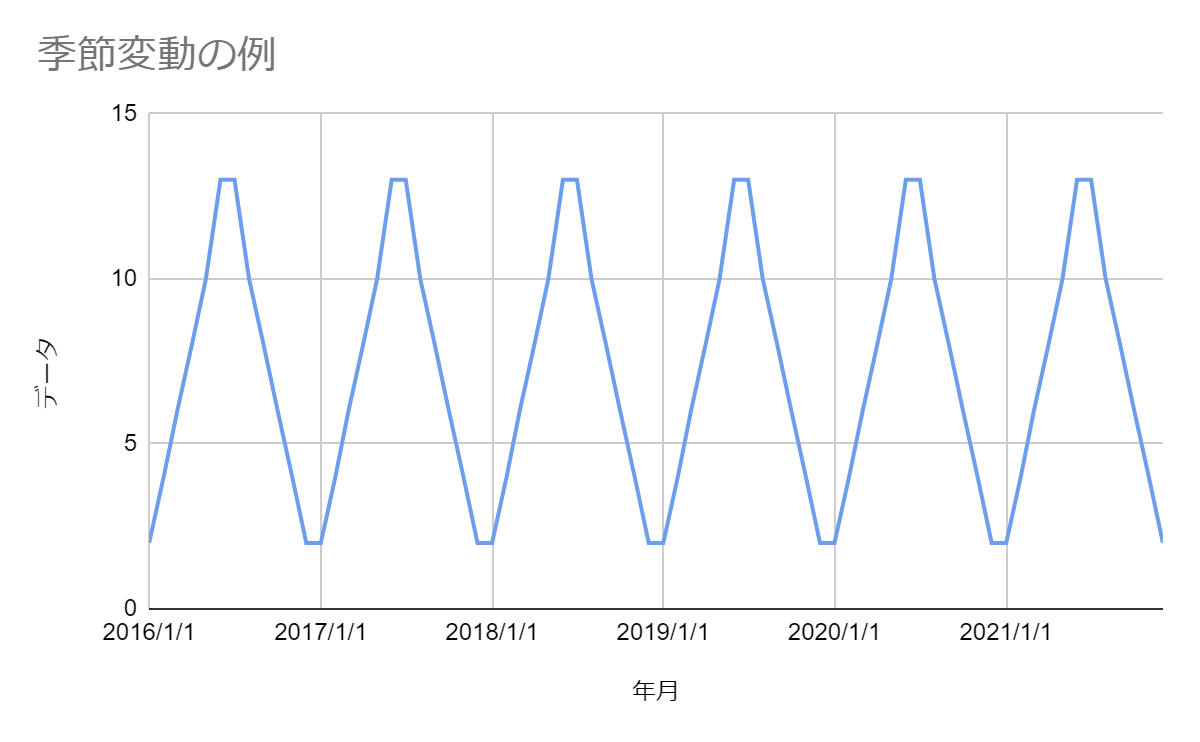
季節変動

季節変動は、季節ごとに繰り返される変動です。

季節変動のスパンは、月や週～1年間ほどの周期が用いられます。

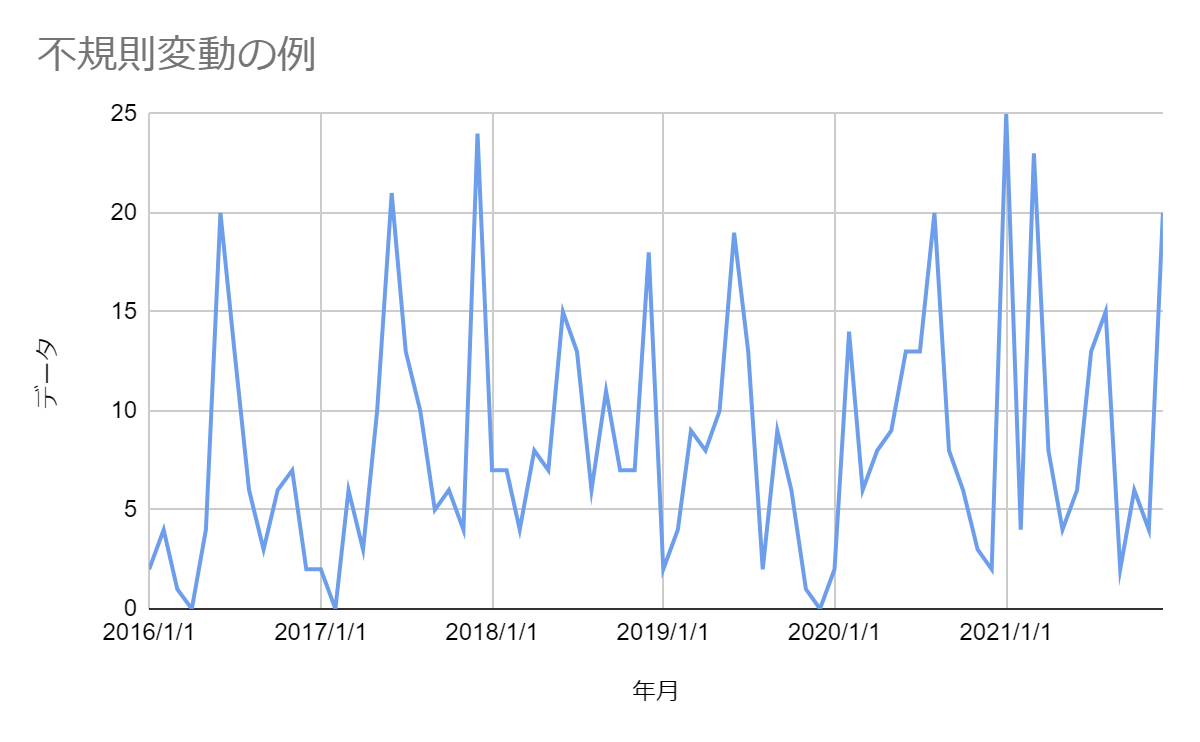
不規則変動

不規則変動は、トレンドや季節変動では説明できない変動です。

突発的変化や有意差が見られない、単なる偶然の変動のことです。

▼関連記事

有意差とは？帰無仮説／対立仮説の考え方とビジネスでの活用を解説 | リサーチコラム

時系列分析の5つの予測モデルの例

これらの「長期変動」「季節変動」「不規則変動」の3つの要因を読み解き、分解する方法として5つのモデルがあります。

１．ARモデル（自己回帰モデル）

２．MAモデル（移動平均モデル）

３．ARMAモデル（自己回帰移動平均モデル）

４．ARIMAモデル（自己回帰和分移動平均モデル）

５．SARIMAモデル（季節変動自己回帰和分移動平均モデル）

これらのモデルは、現実の時系列データの変動や性質を説明するにはそれぞれに限界があります。そのため、それぞれのシーンに合わせて適した予測モデルを選び、それぞれの数式を当てはめることで最適な係数を決定し、精度の高いデータ予測に繋げる必要があります。

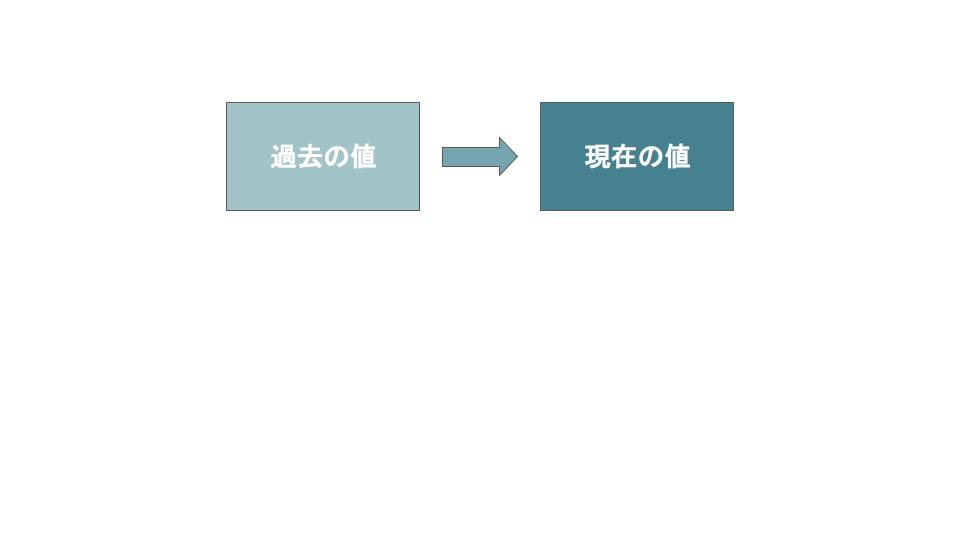
１．ARモデル

AR（自己回帰：Auto Regressive）モデルは、「現在の値は過去の値のみに影響を受ける」と仮定したモデルです。

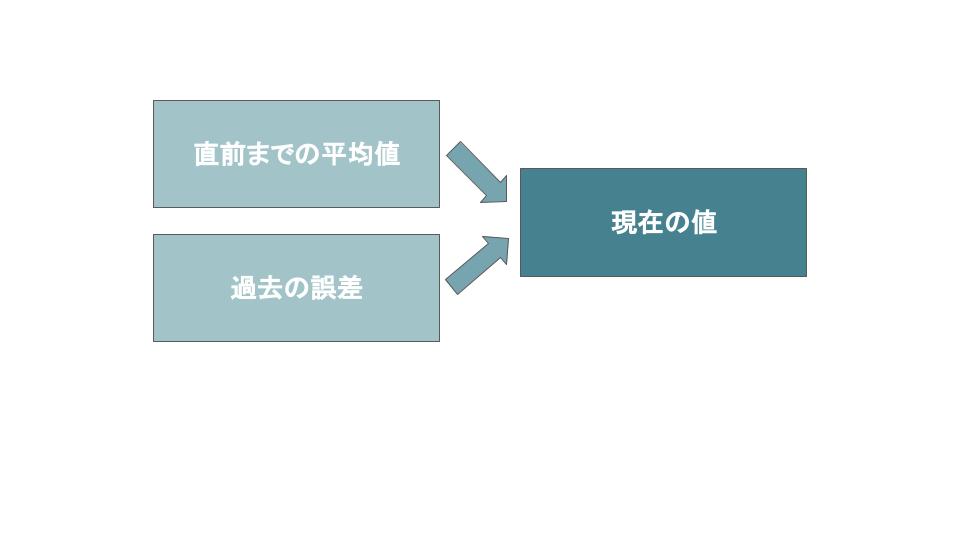
2．MAモデル

MA（移動平均：Moving Average）モデルは、現在の値は、以下の2つに影響を受けると仮定したモデルです。

• 過去の値の平均値
• 過去の誤差（実績値と予測値の差）

直前の平均値とその誤差から、値を予測します。

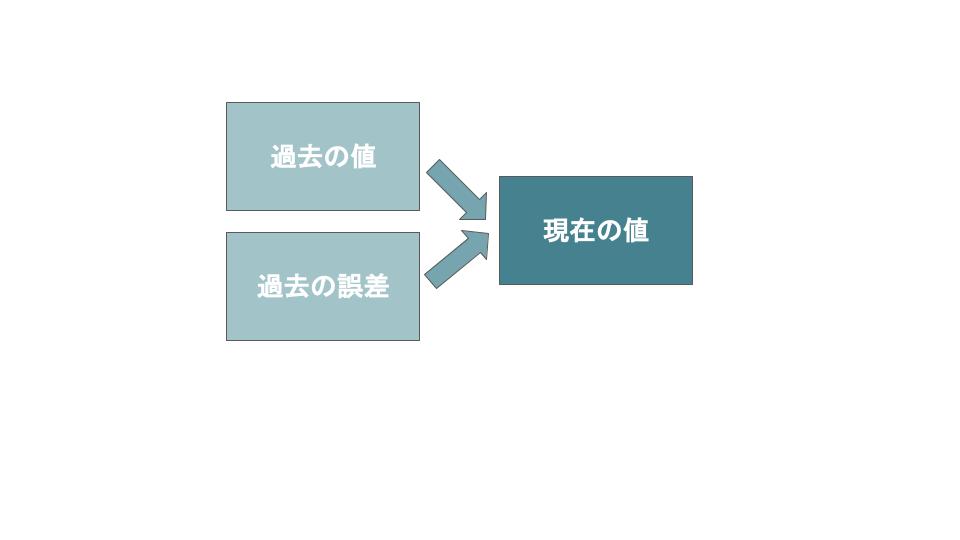
3．ARMAモデル

ARMA（自己回帰移動平均：Auto Regressive Moving Average）モデルは、ARモデルとMAモデルを組み合わせたモデルです。

現在の値は、過去の値とその誤差に影響を受けていると仮定して、分析を行います。

4．ARIMAモデル

ARIMA（自己回帰和分移動平均：Auto Regressive Integrated Moving Average）モデルは、ARMAモデルにおいて長期変動も考慮したモデルです。

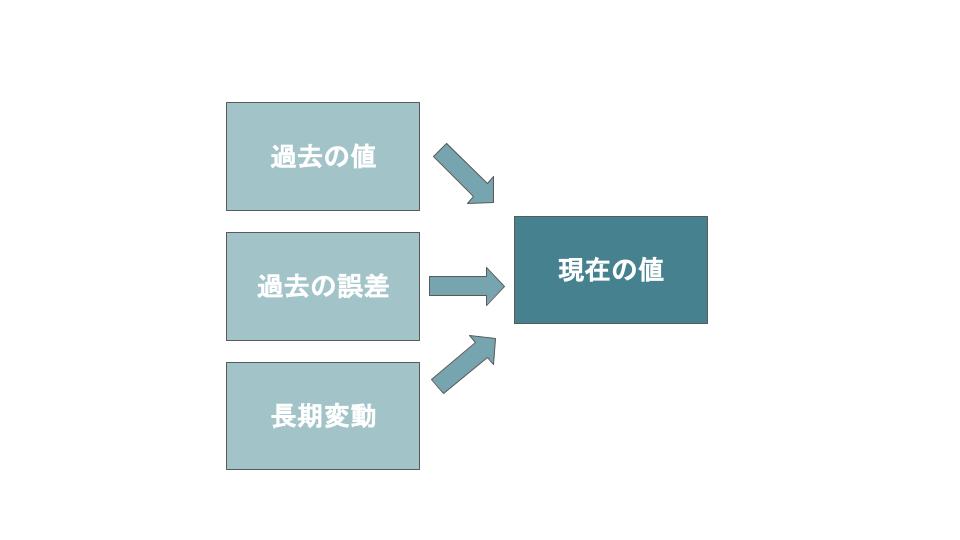
ARIMA（自己回帰和分移動平均：Auto Regressive Integrated Moving Average）モデルは、ARMAモデルにおいて長期変動も考慮したモデルです。

これにより、各時期のトレンド要因部分とARMA部分を結合させて分析できるため、トレンドと季節性両方を考慮できることが特徴です。

5．SARIMAモデル

SARIMA（季節変動自己回帰和分移動平均：Seasonal Auto Regressive Integrated Moving Average）モデルは、ARIMAモデルに、追加で季節性を考慮したモデルです。

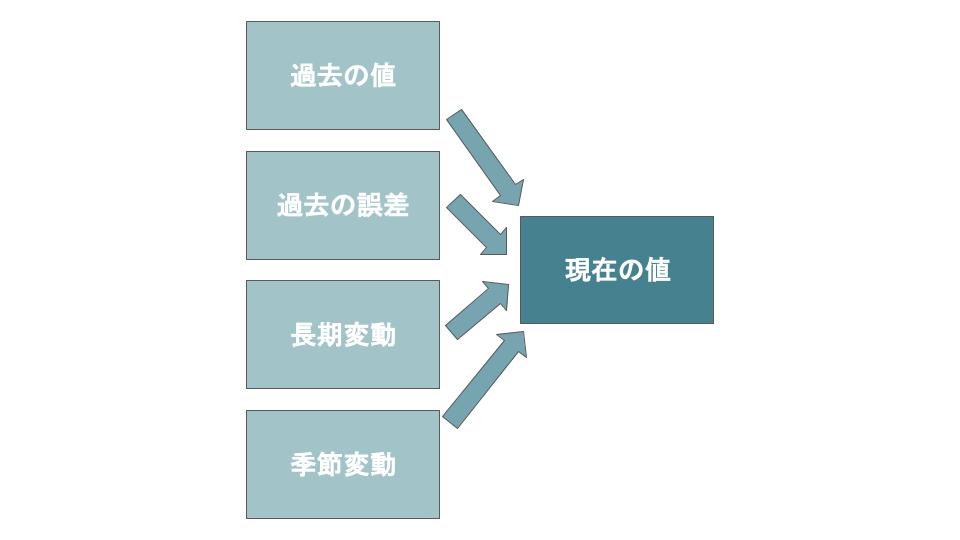
時系列変化と季節変動を、それぞれARIMAモデルで分析することで、過去のデータから現在の値を予測します。

膨大なパターンの数式を用いて分析を行う必要があるため、12カ月など、あらかじめ決めておいた周期で分析を行うことがおすすめです。

まとめ

時系列分析は、時間経過に伴って変化するデータを、長期変動、季節変動、不規則変動のどの要因が影響しているのか分類した上で、統計学的手法で分析し、将来のデータを予測する手法です。

この記事では、時系列分析の意味や時系列分析モデルの例などを解説しました。企業に存在する数多くの時系列データから新しい価値を生むためにも、時系列分析を活用しましょう。