多変量解析とは、複数のデータ（変数・変量）の関連性を分析し、データを要約・予測するための分析手法の総称です。 ある特定の分析手法を示すものではなく、重回帰分析や主成分分析など多くの分析方法を含んでいます。

多変量解析は、マーケティングの場面でも頻繁に活用されています。

多変量解析の考え方や分析手法を知ることで、自社が求めたい結果に応じた使い分けが可能になり、すぐに役立つような多面的で実践的な分析結果を得ることも出来ます。

多変量解析とは？

これまでに、1変量解析やクロス集計・散布図といった2変量解析を行った経験がある方もいるかもしれません。 多変量とは、1変量や2変量よりもさらにデータ数が多いという意味です。分析手法の数も増えますが、そのぶんデータから考察できる範囲も広まります。

 

出典　株式会社JERA

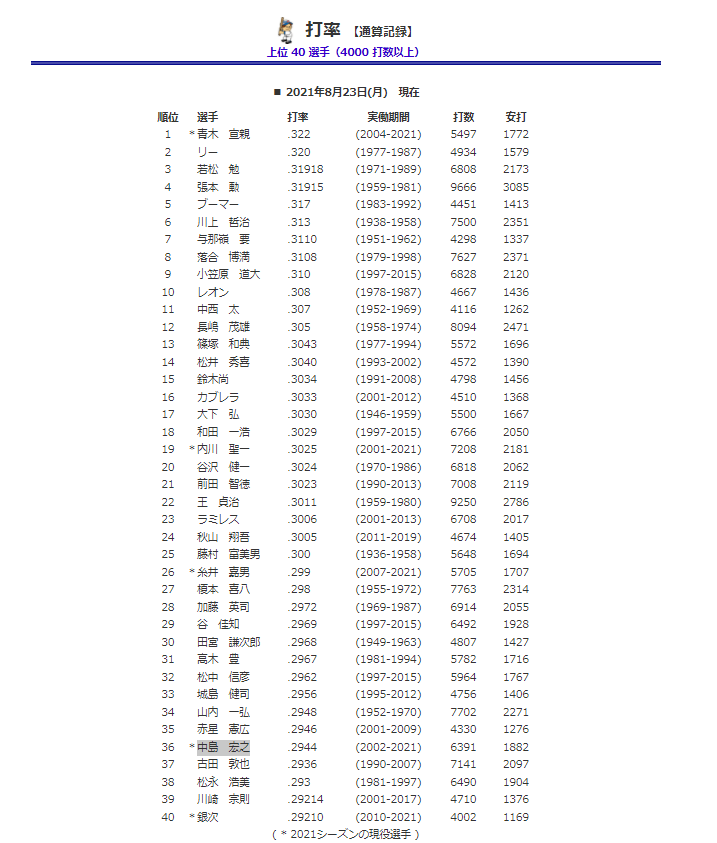
上の図は2020年度のセ・リーグ個人打撃成績です。 横一列に並ぶ「打率」「試合」「打席」「打数」…といった複数のデータ（変数）はそれぞれ眺めるだけではなかなか関係性が読み解きにくいものです。

こういった複数のデータの関連を読み解きたいとき、多変量解析は役に立ちます。
例えば「優れた野手にはどのような傾向があるのか？」「出場した試合数と成績との関係はあるのか？」といった要約や、「◯安打、◯本塁打をとる選手はどれぐらいの出塁率を期待できるのだろうか？」といった予測まで行うことができます。

多変量解析の基礎知識

多変量解析にはさまざまな手法があり、それぞれ分析の目的や扱うデータによって適した手法が変わります。

多変量分析の分析手法の使い分けは「目的（予測で使うのか、要約で使うのか）」そして「種類（データが質的か量的か）」の２点で考えると良いでしょう。

目的・種類で大まかに多変量分析の手法を分類すると、以下のようになります。

多変量解析の２つの目的

多変量解析を行う目的として挙げてきた「予測」と「要約」とはなんなのでしょうか？

目的1．予測

「予測」とは、集めたデータをもとにして、それによって結果がどのようになるのかアタリを付けることをいいます。 例えば、現在の店舗の売り上げや立地、店員数、取り扱い商品数などのデータをもとにして、新店舗の売り上げを見込むことなどが当てはまります。

目的2．要約

「要約」とは、集めた複数のデータを共通項でまとめて分けることをいいます。 商品に関するアンケートをとったとしても、集まった回答を個別に理解するのはかなり難しいものです。サンプルサイズが増えるほど、ひとつひとつを見ていくのはかなりの手間となってしまいます。

アンケート結果の情報を歪めないようにしながら

• どのようなグルーピングができるのか？
• どのような傾向があるのか？

というようにまとめることで理解・取り扱いがしやすくなります。

 

データの種類：目的変数と説明変数／量的・質的について

次に、データの種類を見ていきましょう。 このとき注目するべきデータは、目的変数と説明変数です。

目的変数

リサーチをする上で求めたい項目。例えば「将来の売り上げ予測」など。

説明変数

目的変数を求めるために必要なデータ。例えば「現在の売り上げや顧客数」など。

目的変数と説明変数は、例えば、「今年9月の予想の店舗売り上げ（＝目的変数）を求めるために、去年9月の店舗売り上げや顧客数など（＝説明変数）を参考にする。」といった関係性になっています。

目的変数と説明変数はそれぞれ「量的」「質的」に分けられます。

量的データ（定量データ・数量データ）

数値で表せるデータ。例えば「人数」「実際の売り上げ」など

質的データ（カテゴリデータ・定性データ）

数値で表すことができないデータ。例えば「好き・嫌い」「楽しい・悲しい」など

このとき、予測を目的とする分析であれば、目的変数のデータの種類が質的か量的かを気にする必要があります。 しかし、要約を目的とする分析であれば、目的変数のデータの種類は関係なく、説明変数の種類のみで決定します。

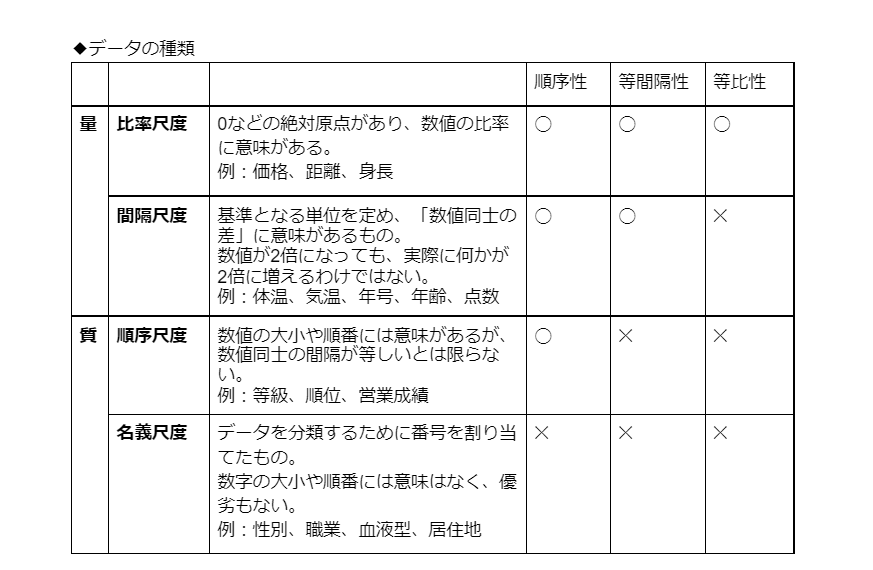
◆基本的な分析手法の一覧表

ちなみに、量的データ＝数値、質的データ＝言葉、と考えてしまう方がいるかもしれませんが、必ずしもそうではありません。

質的データであっても、便宜上番号を割り振ることがあったり、量的データであっても実際には比率に意味がなかったりすることがあるからです。
この場合、数字であらわされていても、比較したり計算したりすることに意味がありません。 これは「尺度」という考え方であらわされます。尺度は以下の4つに分かれています。

多変量解析の代表的な分析方法

多変量解析の各手法について解説していきます。

主な分析手法の名称	概要説明
重回帰分析	収集データをもとにして、ひとつの結果を求める
コンジョイント分析	商品の各評価項目がどのくらい購入に影響しているか求める
判別分析	データの分類基準を分析する
ロジスティック回帰分析	収集データをもとにして特定の結果が発生する確率を求める
主成分分析	収集データが大量に存在する場合に用いる
多次元尺度構成法	自社のポジショニングを視覚的に把握する
クラスター分析	集団の中で似ているもの同士をまとめて分類する
因子分析	収集データを分析し、それが収集できた背景要因を分析する
コレスポンスデンス分析	集計結果を散布図に落とし込んで結果をわかりやすくまとめる
数量化I・II・Ⅲ類	収集データが数値で表せないものの場合に用いる

多重回帰分析

重回帰分析

収集したいくつかの説明変数をもとにして、ひとつの目的変数を求める分析手法。多変量解析の分析手法の中で最もメジャー。

例えば、現在「A」「B」という2つの営業所があるとします。 今度「C」という新しい営業所を設立することになり、「A」「B」のこれまでの年間売り上げをもとにして、その「C」の年間売り上げを予測することになりました。 この場合は、

• 説明変数＝「A」「B」の売り上げ
• 目的変数＝「C」の売り上げ予測

ということになります。

コンジョイント分析

 

コンジョイント分析

消費者が複数の商品の中から品物を選ぶときに、「商品の各評価項目がどれくらい購入の意思決定に繋がっているのか？」ということを分析する手法。

例えば、複数の新車が並べられており、この中から一台を選んで購入しようと考えているとしましょう。 この場合、新車を選ぶ基準としては以下が考えられます。

1. 全体のデザイン
2. カラー
3. 燃費
4. 広さ
5. 安全機能
6. 価格

人によって、これらの項目の中でどれを重視するのかは違います。

コンジョイント分析では、こうした商品の条件を「コンジョイントカード」に書き、重視している項目順に選んでもらうことで、どの条件がどれくらい重視されているのかを調査できます。

判別分析

判別分析

いくつかのカテゴリに分類されているデータを見て、「そのデータはどのような基準で分類されているのか？」ということを分析する手法。分類の基準を予測することで、まだカテゴリーに属していないデータを分類するときに役立つ。

例えば、以下を「2つのカテゴリー」として考えてみましょう。

• 自社商品を何度も購入している（リピーターである）
• 自社商品を1回だけ購入して終わった（リピーターにならなかった）

この2つのカテゴリーに属する方々を分析し、購入者の年齢層や職業、世帯人数などを調査します。

これらの情報を分析することで、「リピーターになる・ならないの基準は何か？」ということがわかります。 この基準が判明することで、これからどのような層に商品をアピールすればリピーターが増やせるのかを割り出せるのです。

ロジスティック回帰分析

 

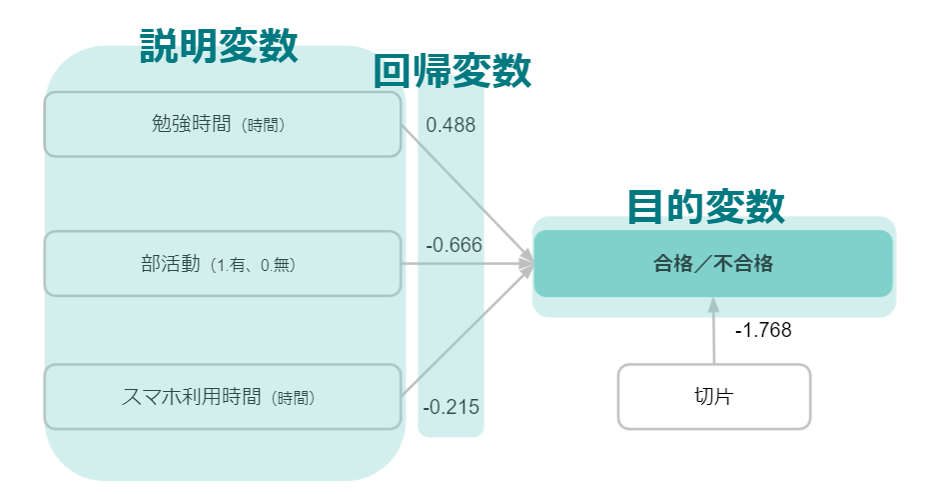
ロジスティック回帰分析

収集してある複数の説明変数をもとにして、特定の目的変数が発生する確率を分析する手法。

例えば、ガンが発生する確率について考えてみましょう。 これまで「ガンになった人・ならなかった人」に関して、以下のデータを集めます。

• タバコの喫煙年数
• 飲酒量

上記の2つは説明変数です。これらの説明変数を分析することで、「喫煙年数や飲酒量がどれくらいあるとガンになる確率が高くなるのか？」ということがわかります。

この基準が判明することで、ガンかどうかを調査したい方の喫煙年数と飲酒量をもとにして「どれくらいの確率でガンにかかっているのか？」を割り出せるのです。

主成分分析

主成分分析

量的な説明変数がたくさん存在する場合に用いる分析手法のこと。量的な説明変数の数が多すぎると分析の手間がかかるため、説明変数をいくつかの「主成分（カテゴリー）」ごとに分けることで、少ない要素でまとめられる。

例えば、ウォーターサーバーを利用した感想を聞いた結果、以下のアンケートが取れたとしましょう。

1. 水に臭みが無くて飲みやすい
2. 喉越しがスッキリしている
3. 水を注ぐボタンが押しにくい
4. どこにボタンがあるのかわからない
5. 部屋のインテリアとしても使えるデザインだった
6. 家具のひとつとして活用できそう

これらをまとめると以下のようになります。

• 1,2→味や食感がとても良い
• 3,4→機能性に難あり
• 5,6→デザイン性が高い

このように、説明変数同士を見比べて適切な主成分（カテゴリー）に分けることで、情報の正確性を損なわないようにしつつ、データの全体像を把握しやすくなるのです。

多次元尺度構成法

多次元尺度構成法

主に自社のポジショニングを視覚的に把握するために用いられる手法。

例えば自社で新商品を発売した際に、消費者に対してアンケートを取り「既存商品との違いはどのくらいあるのか？」ということを評価してもらいます。

その結果を多次元尺度構成法を用いて視覚的に落とし込むことで、

• どれだけ消費者に差別化ポイントが伝わっているのか？
• どういう点で差別化を感じ取ってもらえているか？

などを知ることができるのです。

クラスター分析

クラスター分析

さまざまな属性のものが混ざり合っている集団の中で似ているもの同士をまとめて、グループに分類する分析手法。意識・価値観・嗜好などの「ハッキリとした線引きがないもの」を分類できる。

例えば、以下のような質問項目があったとしましょう。

1. あなたは人に優しい人間だと思いますか？
2. 毎日の生活に刺激がほしいと思いますか？
3. 仕事に打ち込んで自分の能力を高めていきたいと思いますか？

こうした質問に対して5段階評価を設定することで、人の考え方という数値化困難なものを視覚化して把握できるようになるのです。

因子分析

因子分析

収集した説明変数を分析し、そのようなデータが収集できた背景要因を分析する手法。

例えば、学校で5教科に関するテストを行いその結果が公表されたとしましょう。これによって「生徒が各教科で何点を取れたか？」という説明変数は集まります。

しかし、これだけでは「どういう要因があってこのような点数を取れたのか？」という部分まではわかりません。これを分析するために活用するのが因子分析です。

コレスポンスデンス分析

コレスポンスデンス分析

クロス集計結果を散布図に落とし込むことで、調査結果をわかりやすくまとめるための分析手法。

例えば、社内食堂を利用している人に以下の項目を聞いたとしましょう。

1. 直近1ヶ月間で食べた社内食堂のメニューは何ですか？すべて選んでください。
2. あなたの年代を教えてください。

これを散布図に落とし込むことで、どの年代にはどういったメニューが好まれているのかが一発で確認できます。 もちろん、すでにクロス集計表に落とし込まれているので、それを読めば把握できないことはありません。

ただし、アンケート項目がさらに膨大になると、クロス集計表で見るのはかなりの手間になります。 散布図に落とし込んでおけば、膨大な量になっても視覚的に把握できるので分析が楽になるのです。

 

数量化I・II・III類

数量化I・II・III類

分析手法のうち、以下に対応している分析手法のこと。

1. 数量化I類：重回帰分析
2. 数量化II類：判別分析
3. 数量化III類：主成分分析あるいは因子分析

重回帰分析・判別分析・主成分分析・因子分析では、説明変数に「量的データ」を用いていました。しかし、それでは数値化可能な変数を用いてしか分析ができません。

この「数量化I・II・III類」を用いることで、それぞれ対応している分析手法の説明変数が「質的データ」になって対応できるようになります。

例えば、数量化I類に対応している「重回帰分析」の説明で出した例を考えてみましょう。重回帰分析の場合はそれぞれの変数が以下のようになっていました。

• 説明変数＝「A」「B」の売り上げ
• 目的変数＝「C」の売り上げ予測

この場合、説明変数は明確に数値として出ているので量的データです。 それでは、この説明変数をこのように変更すると、どうなるでしょうか？

• 説明変数＝これまでの「A」「B」への評判
• 目的変数＝「C」の売り上げ予測

「会社の評判」というものは数では表せません。「あそこのサービスはまあまあ良い」「品揃えが悪いから系列店には期待していない」などを数で測定するのはかなり困難ですよね。つまり「質的データ」になったといえます。

しかし数量化I類を用いて分析することで、「評判」をさらにいくつかのカテゴリーに分類し、それぞれの適切なウェイトを考慮することで計算できるようになります。 このように、質的データであっても数量化を行うことで、適切に説明変数を扱うことができるのです。

多変量解析はどのような手順で分析を行うのか？

多変量解析は、基本には1変量解析・2変量解析を経てから行われます。 なぜなら、収集したデータでいきなり多変量解析を行うと多変量解析に適したデータになっておらず、かなり複雑になることが予測されるためです。

1．データ収集

まずは、アンケートを実施したり店舗の売り上げ情報を集めたりして解析するもととなるデータを手に入れます。 このとき、同時に以下を決めておくとスムーズに解析に取り組めます。

このデータ収集の段階で「データクリーニング（エディティング）」も行いましょう。データクレンジングとは、収集したデータをチェックして、矛盾や回答の抜け漏れなどが無いかを確認する作業です。

2．1変量解析（単変量解析）

まずは、ひとつの変数だけを用いて「1変量解析（単変量解析）」を行いましょう。 例えば「新店舗の売り上げ予測」のために以下のデータなどを収集したのであれば、この中からひとつだけを選んで分析するということです。

データをひとつ選んだら、以下の処理を行います。

1. 外れ値の検出
2. 異常値の処理
3. 分布状況を確認する

1.外れ値の検出

「外れ値」とは、データの値を見たときに、多くの値が分布している箇所との差が大きいため「正常ではない」と判断できる値のことをいいます。 とはいえ、データの集団から外れているからといって、即座に外れ値として切り捨ててはいけません。

例えば、1日に飲む水の量についてアンケートを取ったとしましょう。データの数としては「1〜2リットル/日」という数値に集中していたとしても、「4リットル/日」というデータを切り捨てるべきではありません。 確かにメインとなる値の集団からは外れていますが、実際に飲んでいる人が存在しているため正常値なのです。

2.異常値の処理

もしも外れ値の中に、明らかにおかしいと思われる「異常値」があった場合は速やかに外しましょう。 極端な例ですが、1日に飲む水の量を「1,000リットル」と回答している場合、明らかに記入ミスだということがわかります。

3.分布状況を確認する

外れ値や異常値に関しては、数値だけを眺めていてもなかなか検出できません。そのため、箱ひげ図やヒストグラムなどを活用して、数値を視覚的にわかりやすくして判断をします。

3．2変量解析

「2変量解析」では、上記の1変量解析で行ったことを2つのデータで行います。 まずはデータ同士の相関性を調べ、それをクロス集計表や散布図などを用いて視覚化し、外れ値や異常値を確認します。 とくに散布図を用いると、値の関係性が即座に把握できるので非常に便利です。

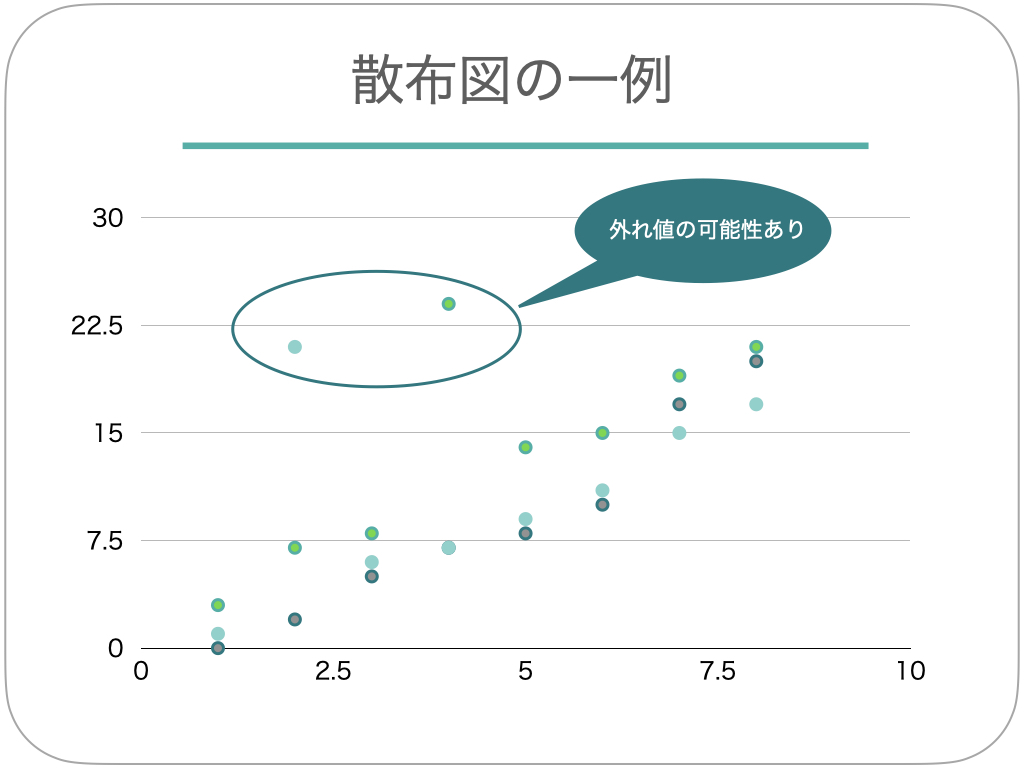
4．多変量解析

2変量解析まで終了したら、次は多変量解析に取り掛かります。多変量解析に関しては、専門の分析ソフトで行います。

Excelといった表計算ソフトでも行えますが、データ量が膨大になるとかなりの手間がかかってしまうためおすすめしません。

まとめ

多変量解析はデータから考察できる範囲も広く、実践的に使いやすい分析手法です。ビジネスの売り上げ予測をはじめとして、さまざまな場面で活用できます。 マーケティング施策にすぐに役立つ分析を行うためには、目的とデータの種類に合わせて適切な分析手法を用いることが大切です。