外れ値の意味と求め方を解説|必ずしも除外することが正解とは限らない?
2023年07月21日
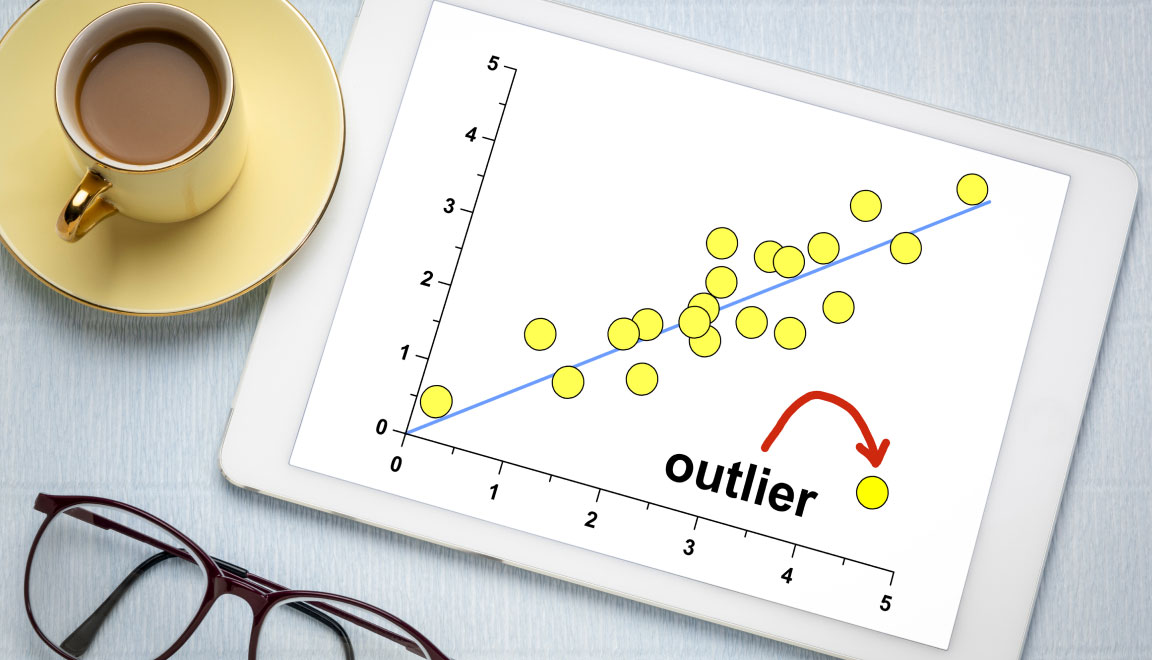
日々の業務でデータ収集を行っていると、他のデータと比較して極端に大きい(もしくは小さい)データを目にすることがあるのではないでしょうか。
他のデータと比べて極端な値のデータのことを、外れ値と呼びます。外れ値を含んだままデータ分析を行うと、外れ値に引っ張られて分析結果や傾向が変わってしまう場合があるため、取り扱いには注意を要します。しかし、場合によっては外れ値を分析することで、重要な知見が得られることもあるため、一概にすべて除けばよいとも言い切れません。
この記事では、外れ値の意味や判定方法、取扱方法について、初心者でもわかりやすいように解説しています。また、エクセルで外れ値を判定する方法も紹介していますので、参考にしてみてください。
- 3分で読めるGMOリサーチ&AIのサービス
-
マーケティング活動では、消費者ニーズに関するデータを収集・分析することがますます重要になっています。GMOリサーチ&AIは、消費者に関するデータを収集できるサービスを、多数提供しています。
【サービス例】
- オンラインリサーチ
- 海外調査
- 消費者インサイト など
あなたの会社でも消費者のデータを収集・分析して、マーケティング活動のクオリティを高めませんか?
- 資料ダウンロード
外れ値とは他のデータと比べて極端に離れた値
外れ値とは、「他と比べて極端に小さな値、あるいは極端に大きな値」のことです。マーケティング調査や実験などでデータを取っていると、他のデータとは大きく異なる(かけ離れた)データが得られることがありますが、これが外れ値と呼ばれるデータになります。
外れ値が生じる要因はさまざまです。例えば測定ミスやデータ転記時のミス、最初から外れ値を入れた状態で母集団が設定されていることで現れることがあります。
異常値との違い
外れ値と似た用語に、「異常値」があります。
外れ値と異常値は、いずれも英語では同じ”outlier”と示します。そのため、両者を同義とする説もあります。
▼外れ値と異常値を同義とする例
「異常値(外れ値outfilterという言い方とほぼ同じ)」と記載
(「基礎統計学Ⅰ統計学入門(東京大学教養学部統計学教室編)(P.30)」より)
ただ、入力ミスや特別な事情など、外れ値のなかでも原因が明確なものを「異常値」と呼ぶことがあります。異常値の例として、プロスポーツチームの観客動員数を例に、考えてみましょう。
あるプロスポーツチームでは、通常の主催試合における観客動員数が数百人程度でした。しかし、世界的に有名な海外選手が入団したところ、その選手のデビュー試合だけは、観客動員数が約2千5百人と、通常の数倍になったのです。
観客動員数が通常の数倍になったのは、超大物選手がデビューしたことと想定されるため、原因は明確です。このときの観客動員数は「異常値」といえます。
外れ値がデータ分析に及ぼす影響
外れ値は、適切に取り扱わないとデータ分析精度が低下するおそれがあります。
先述したように外れ値とは、他と比べると大きく異なる値のことです。平均値や相関係数など、統計指標を測る際に外れ値が混在すると、分析結果にゆがみが生じるおそれがあります。
ただし、場合によっては外れ値を分析対象とすべきケースもあります。そのため、一概に除外すればよいとは言い切れないため注意が必要です。
外れ値はどのように判定する?代表的な4つの方法を解説
外れ値の判定は、「明らかに離れた数値だから、これは外れ値だろう」と主観で行うことは危険です。主観で判断すると、判定する人やタイミングによって、判定結果が異なってくる可能性があるためです。以降、外れ値の判定方法として、代表的な方法を4つ解説します。
標準偏差を用いた判定
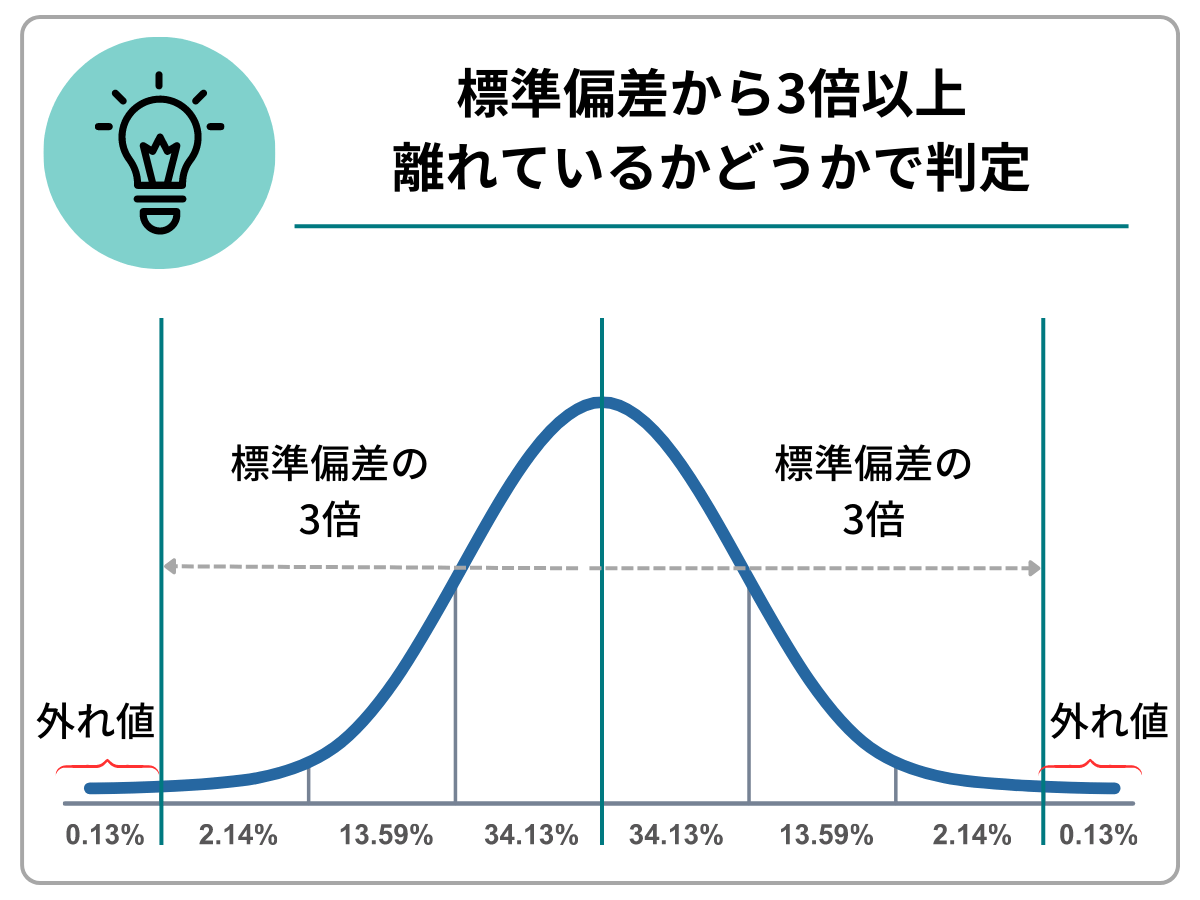
標準偏差とは、データが平均値からどれぐらい散らばっているかを示す指標です。標準偏差を用いることで、外れ値かどうか判定することができます。
よくある判定方法は、標準偏差の値から3倍以上離れているかどうかを基準とし、3倍より外れたものを、外れ値と見なす方法です。
ただし、標準偏差を用いて外れ値を判定する場合は、極端な外れ値に引っ張られる可能性に注意しなければなりません。
なお、標準偏差については、「標準偏差とは?ビジネスでの活用方法と求め方を解説」にて詳しく解説しています。
箱ひげ図(四分位範囲:IQR)
箱ひげ図は、データを大きさ順に並べた際の分布を示しており、四角い箱の上下(もしくは左右)に、ひげが生えている形を取るのが特徴です。
▼箱ひげ図を用いた外れ値の判定
-
- データを大きいものから順番に並べて4等分する(分割点が四分位数)
- 「四分位範囲(IQR)=第3四分位数(Q3) - 第1四分位数(Q1)」
-
- ひげの右端を求める
- 「第3四分位数+1.5×IQRより小さい最大値」
-
- ひげの左端を求める
- 「第1四分位数-1.5×IQRより大きい最小値」
-
ひげの範囲から外れた値が外れ値
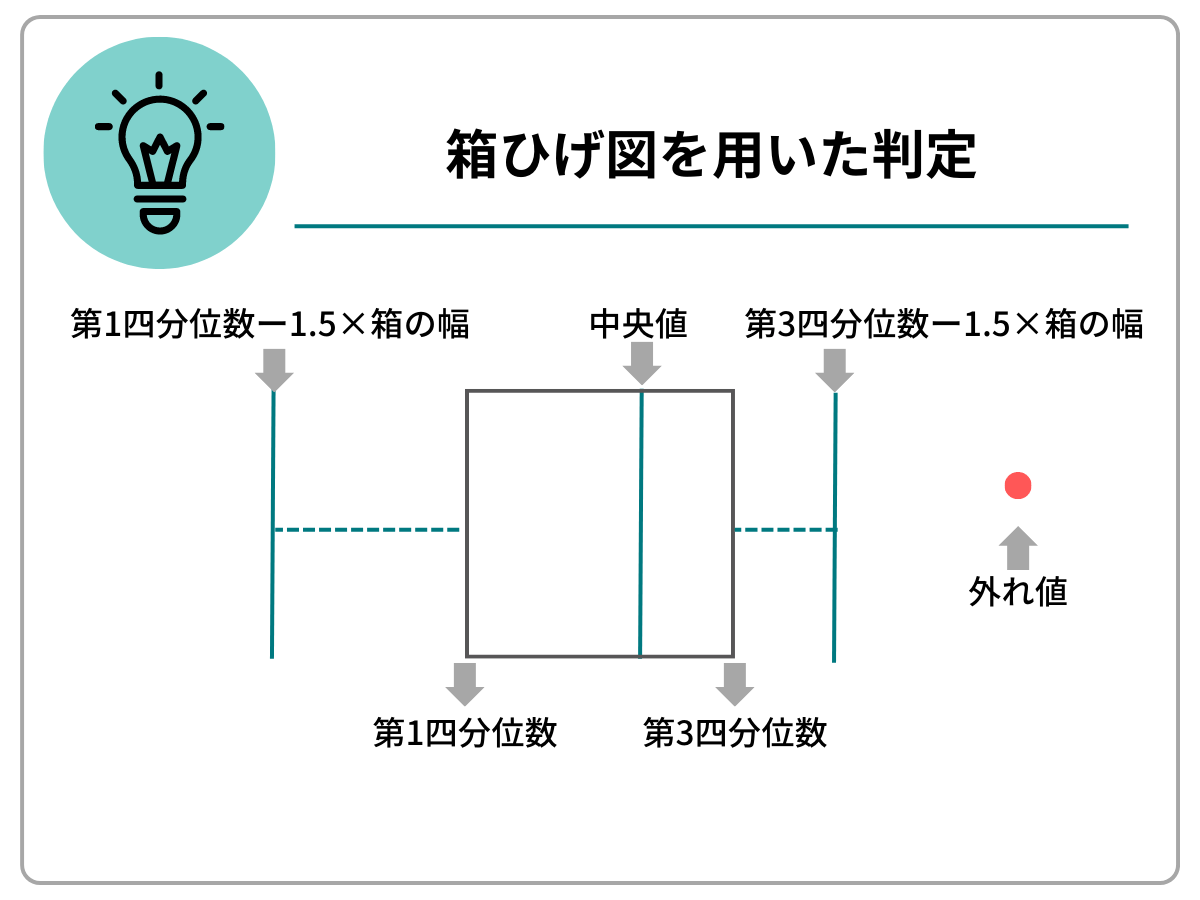
箱ひげ図による外れ値の判定は、データが分散している場合には有効です。しかし、データが中央に密集していると、四分位数の間隔が小さくなってしまうため、うまく判定できなかったり、データ全体で数多く外れ値が発生したりする可能性があるため注意しましょう。
検定
極端に大きいまたは小さい値が見つかった場合、検定を活用することでその値が外れ値か判定する方法があります。外れ値の判定に活用できる検定式は、「トンプソン検定」や「増山の棄却検定」など複数存在しますが、本章では検定の代表例として、「スミルノフ・グラブス検定」を紹介しましょう。
▼スミルノフ・グラブス検定を用いた外れ値の判定
- 「H0:その値は外れ値ではない」と仮定する
※H0:帰無仮説。仮説が正しいかどうか判断するための仮説 - 「(外れ値 - 平均値) / σ」の値を、「有意水準5%」で検定する
- (値を算出した後)外れ値を判定する
※判定時の基準:「スミルノフ・グラブスの棄却検定表」(P6、第3表参照)
クラスター分析
クラスター分析とは、個々のデータから似ているデータ同士をグルーピングする分析手法です。市場調査やマーケティングにおいて、よく使われています。
データ数が一定数存在しており、かつグルーピング方法を間違えていなければ、クラスター内には複数のデータが存在するはずです。しかし、クラスター分析を行った結果、データを1つしか含まないクラスターが見られた場合、他のデータからかけ離れている可能性が高いといえるでしょう。
クラスター分析についてより詳しく知りたい方は、「クラスター分析とは?その手法と応用例を図解!」をご覧ください。
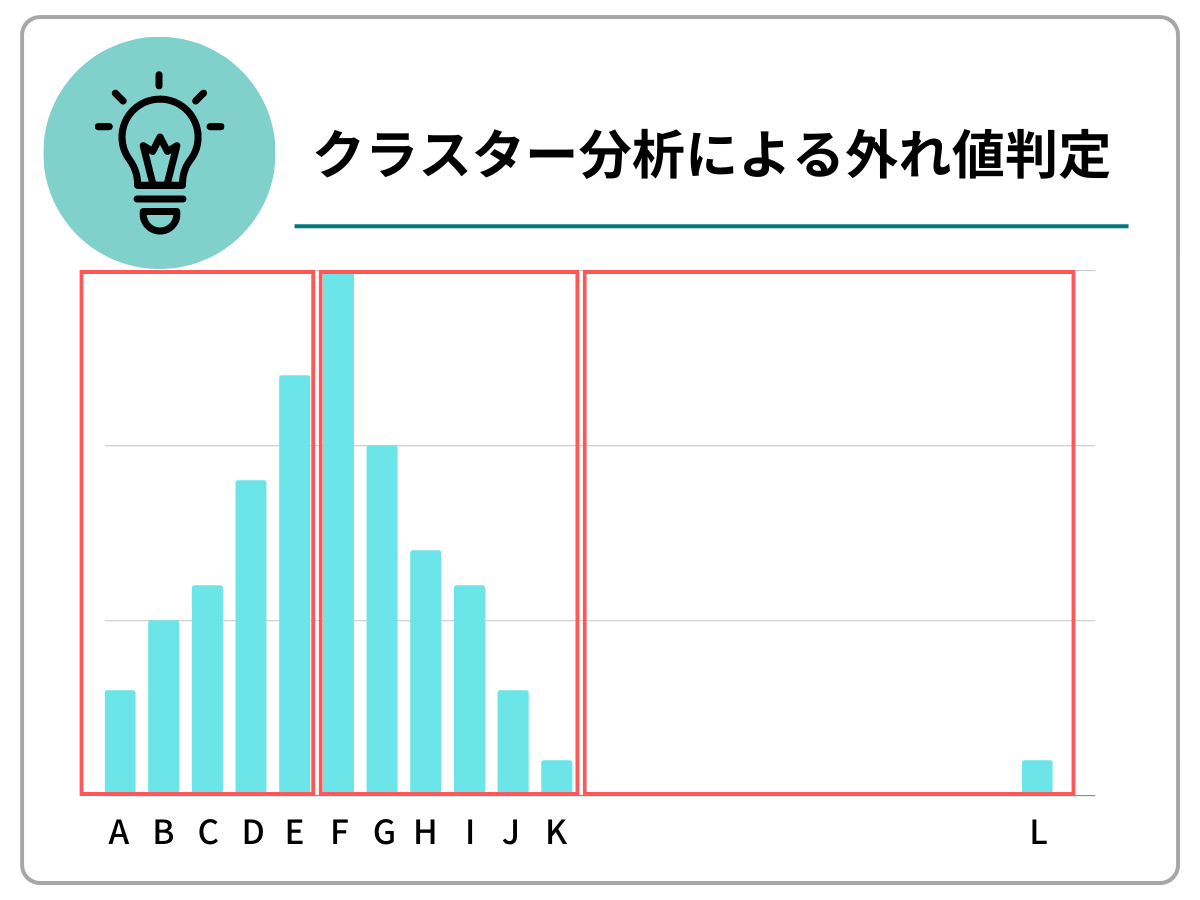
クラスター①:A~Eの値
クラスター②:F~Kの値
クラスター③:①、②以外、Lの値(=外れ値)
【実践】エクセルを用いた外れ値の判定方法とは?
先ほど、外れ値を判定する方法について解説しました。実は、多くの人が触れたことのあるエクセルを用いると、効率的に外れ値を判定することができます。
本章では、先に紹介した「四分位範囲(IQR)での判定(箱ひげ図)」を用いて、エクセルで外れ値を判定するプロセスをまとめます。
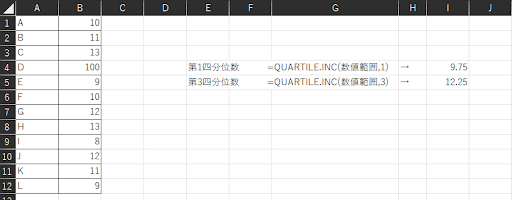
1.QUARTILE.INC関数を使用し、第3四分位数と第1四分位数を求める
エクセルで外れ値を判定するには、「QUARTILE.INC関数」を用います。まずは関数を用いて、第1四分位数と第3四分位数を求めましょう。
▼関数を用いた求め方
| 第1四分位数 | =QUARTILE.INC(数値範囲,1) |
|---|---|
| 第3四分位数 | =QUARTILE.INC(数値範囲,3) |
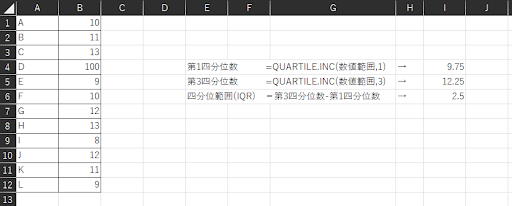
2.四分位範囲(IQR)を求める
次に、四分位範囲(IQR)を求めます。
▼四分位範囲(IQR)の求め方
| 四分位範囲(IQR) | =(第3四分位数)-(第1四分位数) |
|---|
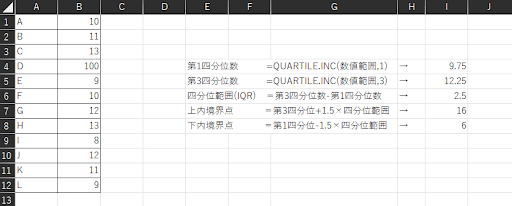
3.判定限界(上内境界点、下内境界点)を求める
四分位範囲(IQR)が確認できた後は、判定限界を確認します。
▼判定限界
| 上内境界点 | =第3四分位数+1.5×四分位範囲 |
|---|---|
| 下内境界点 | =第1四分位数-1.5×四分位範囲 |
4.判定基準を作成する
ここまでのステップで得られた数値をもとに、判定限界の上内境界点と下内境界点が一目でわかる判定基準を作成します。
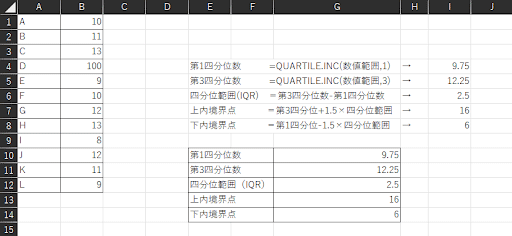
5.照らし合わせ、判定する
最後に、出来上がった判定基準とデータを照らし合わせて、外れ値か否かを判定します。
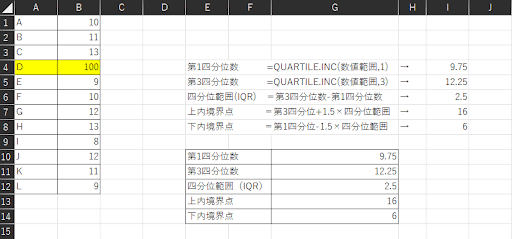
この場合、Dの100のみ下内境界点6〜上内境界点1の間にないため、外れ値となります。
外れ値を扱ううえでの注意点
ここまで、外れ値の意味や求め方について解説してきました。データを扱う過程で外れ値が発生することは珍しくありませんが、外れ値を適切に扱わないと得たい分析結果を正しく取得することができなくなる場合もあります。
以下に2つ、外れ値を扱う上での注意点を解説します。
外れ値=除外対象ではない
人によっては、外れ値は分析結果に影響を与えてしまうため、全て除外してしまえばよいと考えるかもしれません。しかし実際には、外れ値は必ずしも除外対象とは限らないことに注意が必要です。
例えば、新生児の体重について研究してデータを取っている過程で、3,000kgの新生児のデータがあったとします。これは明らかに、単位を”g”と”kg”で間違えていますので、除外しても問題ないでしょう。
一方で、珍しいもののあり得ないとは言い切れない外れ値であれば、除外すべきでないかもしれません。例えば、治験による副作用の発生や、車の安全性検証時によるブレーキの効き方は、除外すべきではない外れ値の最たる例でしょう。
有益な外れ値も存在する
外れ値が発生した原因を考察する過程で、重要な知見が得られることもあります。
例えば、あなたが1年間、Youtubeで100本の動画配信を続けたとしましょう。1年後に100本の動画を分析した結果、3本の動画だけPV数が他の10倍以上を記録していたとします。平均から大きく外れた数値はある意味外れ値とも捉えることができますが、その3本についてコンテンツ内容や拡散状況を分析すれば、PV数を増やすヒントを得られるかもしれません。
なお、外れ値を分析する際には、目的に合わせて適切に扱うことが大切です。例えば上記のYoutube動画の例であれば、PV数を増やすことが目的なので、各動画のPV数に着目しています。
まとめ|外れ値から有益な知見を得られることもある
外れ値は、「他と比べて極端に小さな値、あるいは極端に大きな値」です。データが外れ値か否かは、箱ひげ図や検定、クラスター分析で判定されます。簡易な判定であれば、エクセルを用いて確かめることもできます。
外れ値を適切に取り扱うことは、データを正確に分析するために欠かせません。かといって安易に外れ値を除外すると、データの精度は高まるものの、必要な情報まで失ってしまう恐れがあります。データ分析の目的を考慮したうえで、外れ値の扱いを考えるようにしましょう。
- 3分で読めるGMOリサーチ&AIのサービス
-
マーケティング活動では、消費者ニーズに関するデータを収集・分析することがますます重要になっています。GMOリサーチ&AIは、消費者に関するデータを収集できるサービスを、多数提供しています。
【サービス例】
- オンラインリサーチ
- 海外調査
- 消費者インサイト など
あなたの会社でも消費者のデータを収集・分析して、マーケティング活動のクオリティを高めませんか?
- 資料ダウンロード
よくある質問
| Q1.外れ値と異常値の違いは? |
|---|
|
外れ値と異常値は、英語では同じ”outlier”です。そのため、両者は同義とする考え方もあります。ただ、両者は異なると考え、外れ値のうち原因が明確なものを「異常値」と呼ぶケースもあります。 詳しくは「異常値との違い」の章をご覧ください。 |
| Q2.外れ値はデータ分析時にどう取り扱えばいい? |
|
明らかなミスが原因で生じた外れ値であれば、除外してもよいでしょう。 ただ、珍しいもののありえないと言い切れない外れ値であれば、あえて除外しない方がよいケースもあります。また、場合によっては外れ値に着目することで新たな知見を得られるかもしれません。 詳しくは「外れ値を扱ううえでの注意点」の章をご覧ください。 |
- サービス概要を無料配布中「3分で読めるGMOリサーチ&AIのサービス」
-
GMOリサーチ&AIはお客様のマーケティング活動を支援しており、さまざまなサービスを提供しております。
- スピーディーにアンケートデータを収集するには
- お客様ご自身で好きな時にアンケートを実施する方法
- どこの誰にどれくらいリーチができるか
ぜひこの機会にお求めください。 - 資料請求する


