サンプル調査では母数から調査対象を抽出して調査を行うため、どうしても誤差が生じてしまいます。サンプルサイズを増やせば誤差を小さくできるものの、扱うサンプルサイズが大きいほどコストも大きくなってしまう懸念があります。そのため、データの正確性とコストの折り合いをどうつけるべきか、悩んだことのある方も多いのではないでしょうか。

そこで役立つ概念が、標準誤差です。標準誤差とは、標本から得られる推定量のバラツキを意味します。

本記事では、標準偏差の活用方法や類語である標準偏差との違いについて、初心者でもわかりやすいように解説しています。エクセルを用いた計算方法も解説していますので、重要なポイントを確認し、実践にお役立てください。

標準誤差とは、標本から得られる推定量のバラツキ

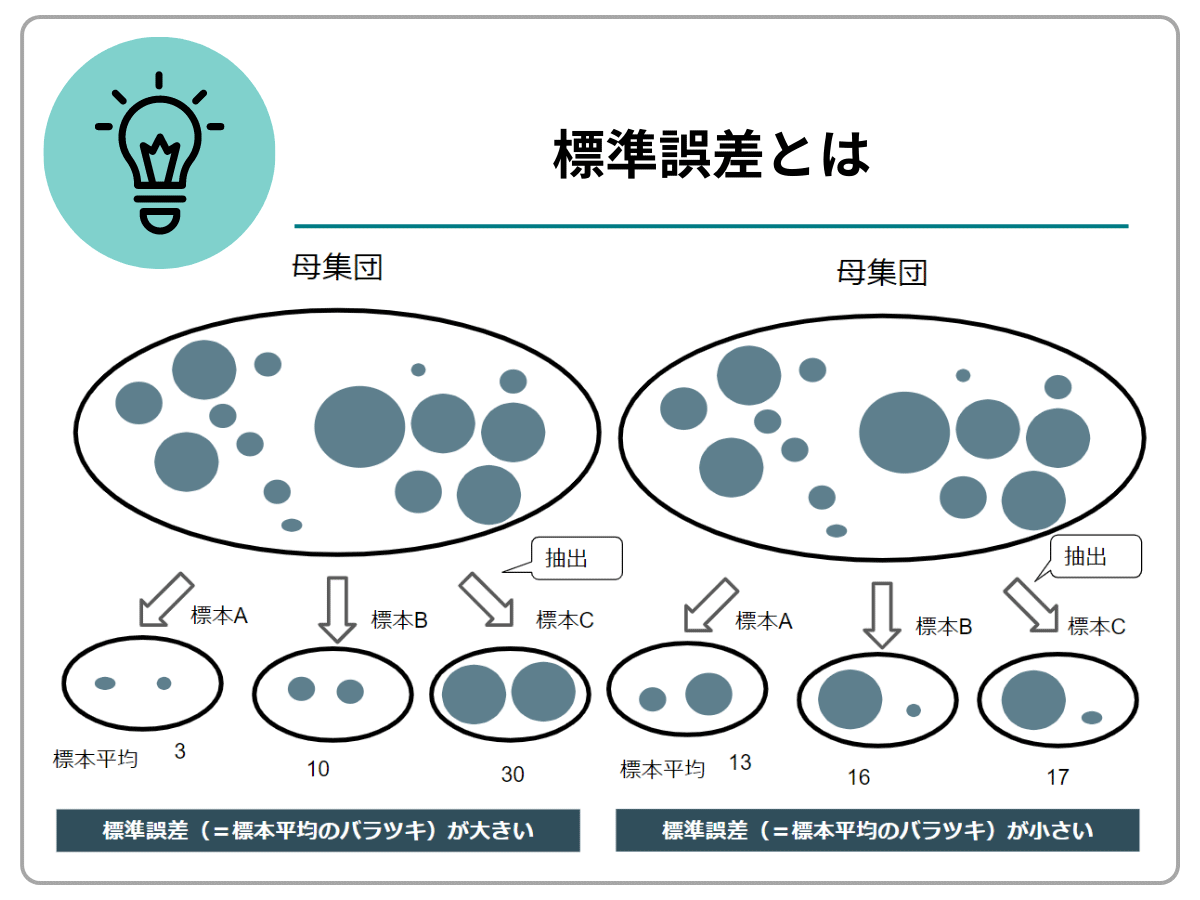
標準誤差（SE：standard error）は、推定量の標準偏差で、標本から得られる推定量そのもののバラツキを指します。標本平均のバラツキが小さければ小さいほど、標本の調査結果は母集団に近くなるため、調査結果の正確度が増すと言えます。

また、サンプルサイズの大きさによっても標準誤差は変動します。サンプルサイズが大きいと、標準誤差は小さくなる性質をもっています。

▼標準誤差の意味

大きい	推定量のバラツキが大きく、精度が低い
小さい	推定量のバラツキが小さく、精度が高い

似ている言葉”標準偏差”とは

標準誤差と似ている言葉に「標準偏差」がありますが、それぞれ意味と計算方法が異なります。標準偏差は、データのバラツキを表す指標であり、あるデータが平均値からどの程度散らばっているかを示します。

▼標準偏差の意味

大きい	データのバラツキが大きい。平均値から遠く離れている測定値が多くある
小さい	データのバラツキが小さい。測定値の分布が平均値の周りに集まっている

標準偏差と標準誤差の大きな違いは、何のバラツキに着目しているか、という点です。標準偏差はサンプルそのものに着目しますが、標準誤差はサンプルの平均値に着目しています。また、標準誤差より標準偏差が大きくなることはありません。

▼標準偏差の求め方

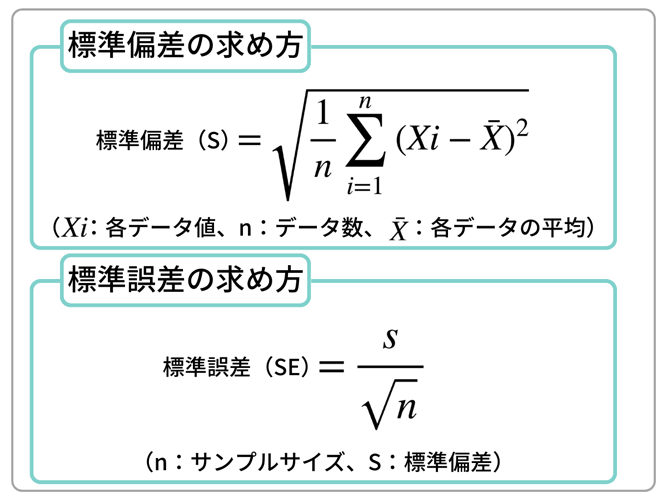
また、エラーバーの見方についても、標準誤差と標準偏差で異なります。

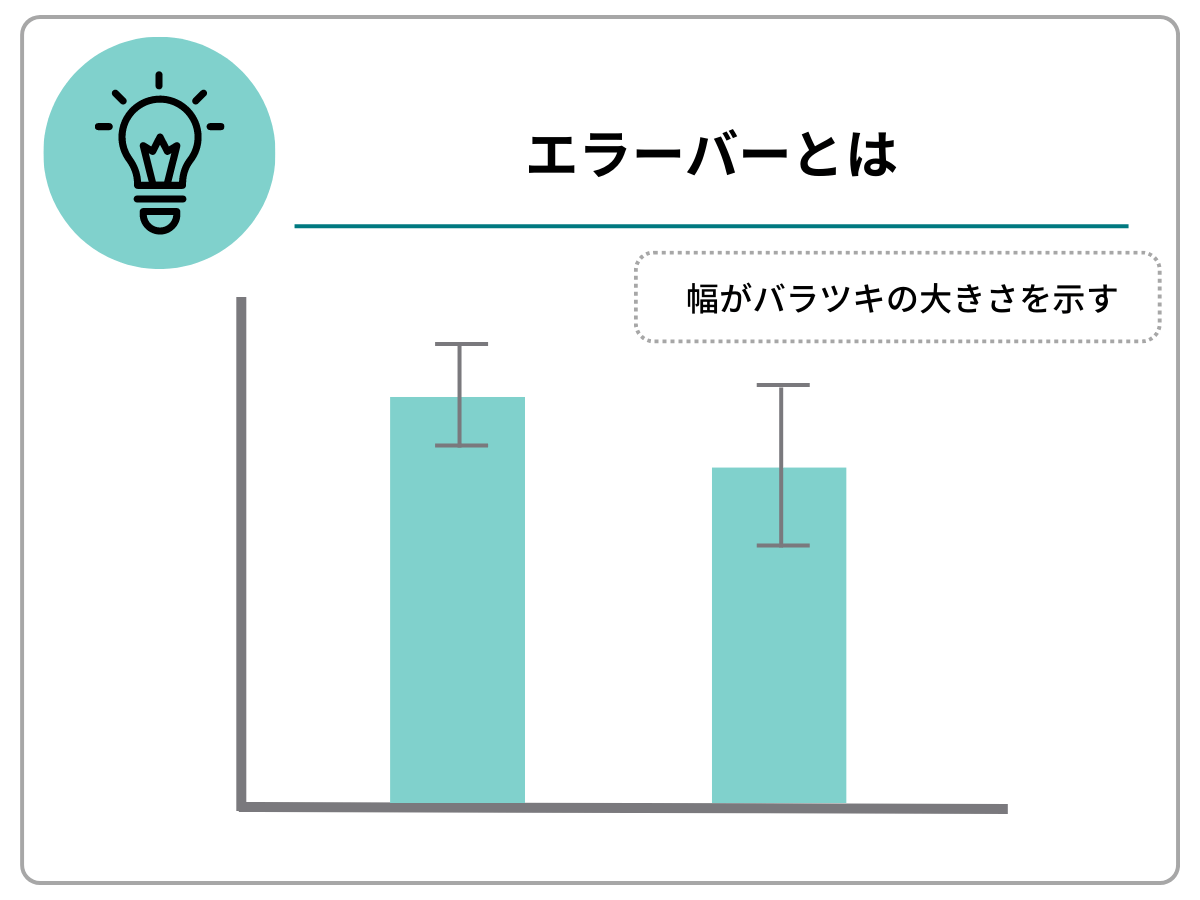
エラーバーとは、データのばらつきを示すグラフです。棒グラフなどを見たときに、グラフに重なる形でI字型の線が記載されているのを見たことがある方もいるのではないでしょうか。このI字型の線こそ、エラーバーです。

標準偏差におけるエラーバーは、平均値±標準偏差を示しています。エラーバーの幅が大きいほど、データのバラツキが大きいことを意味します。

一方、標準誤差におけるエラーバーは、平均値±標準誤差を示しています。エラーバーの幅が大きいほど、推定量のバラツキが大きい、つまり精度が低いことを意味します。

標準偏差については、「標準偏差とは？ビジネスでの活用方法と求め方を解説」にて詳しく解説していますので、あわせてご覧ください。

標準誤差の活用方法

標準誤差を用いると、標本平均のバラツキを知ることができる点について解説してきました。とはいえ、実際の分析の場面でどのように活用できるのか、イメージの持てない方も多いかと思います。

本章では、標準誤差の活用方法について代表的なシーンを2つ紹介します。

正規分布の誤差範囲の決定

標準誤差と信頼区間を活用することで、正規分布の誤差範囲を決定できます。サンプル調査や実験データの分析においては、全数を調査していないことから、誤差の発生は避けられません。しかし、あらかじめ誤差範囲がわかっていれば、真の値に近いかどうか目星をつけられるようになるでしょう。

一般に、サンプルサイズが大きい（n=30以上）場合、標本平均は母平均を中心とした正規分布に従うとされています。これは、サンプルサイズが大きくなるほど元の母集団の平均値に収束するためです。

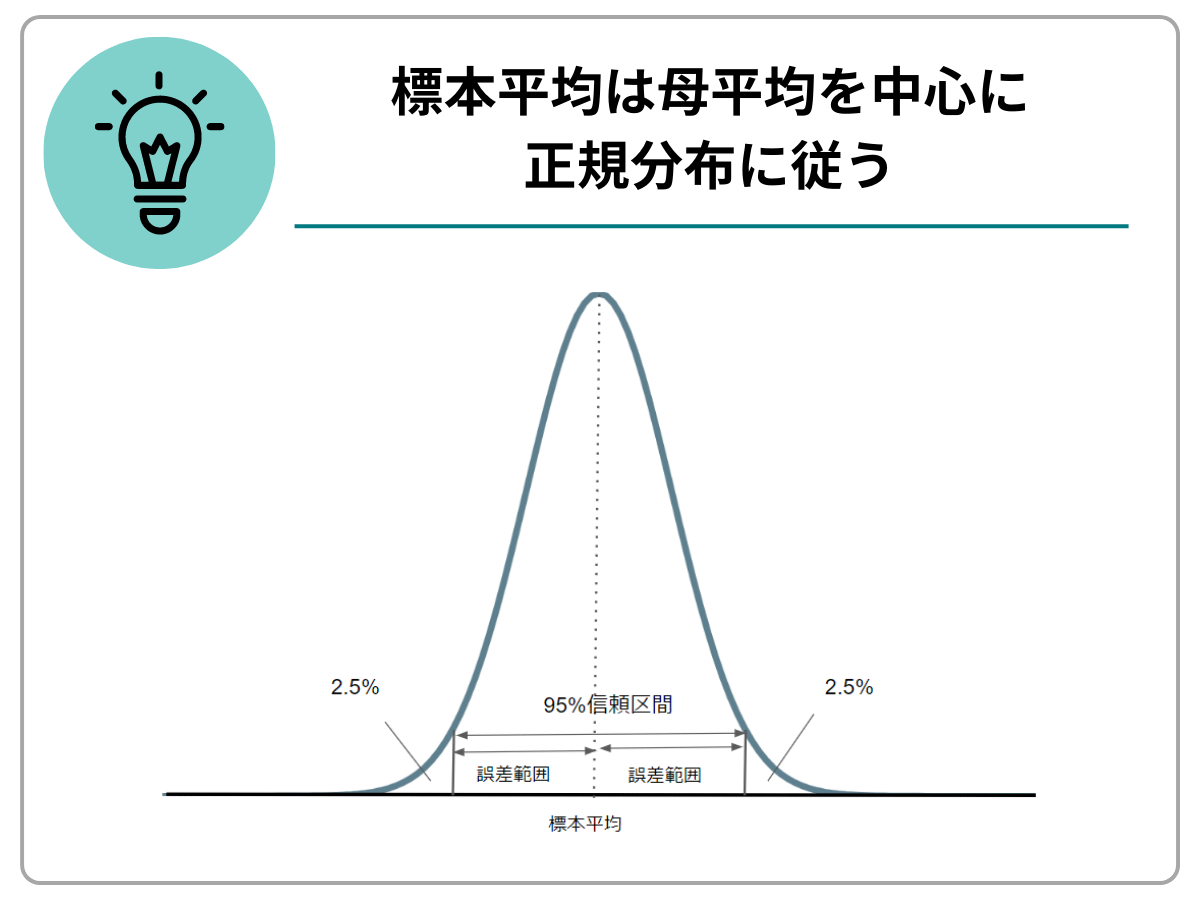
ちなみに、標本平均が正規分布に従うと仮定し、母平均の信頼区間を求める際は、以下の方法にて求めることができます。

▼信頼区間の求め方

95%信頼区間を求める	誤差範囲=1.96×標準誤差
99％信頼区間を求める	誤差範囲＝2.58×標準誤差

必要なサンプルサイズの決定

サンプルサイズを決定したい場合にも、標準誤差を活用できます。

サンプルサイズとは、母集団におけるサンプル（標本）の個数のことです。一般的に、サンプルサイズが大きいほど、調査の信頼性は増すとされていますが、サンプルサイズを大きくすればするほど、調査や分析に要するコストも大きくなってしまいます。

調査の信頼性と必要なコストのバランスをとるためにも、最適なサンプルサイズの設定は重要なポイントになりますが、このとき活用できるのが標準誤差です。

標準誤差を活用すると、分析目的に応じた必要な誤差をあらかじめ設定できます。つまり、正規分布の誤差範囲を満たすサンプルサイズを算出できるようになるのです。

なお、サンプルサイズについて詳しく知りたい方は、「適切なサンプルサイズが調査成功の鍵｜計算方法や決め方を解説」をご覧ください。

標準誤差をエクセルで計算する方法

標準誤差は、エクセルで計算することも可能です。以下に2つ、エクセルを用いて計算する方法を示します。キャプチャ画像を交えて解説しているので、ぜひご自身で計算する際の参考にしてください。

標準偏差と標本数がわかっている場合

エクセルでは、平方根をSQRT()で表現できます。そのため、標準偏差と標本数がわかっていれば、標準誤差を求める式をそのまま使うだけで標準誤差の計算が可能です。

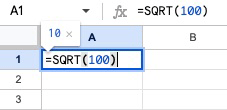
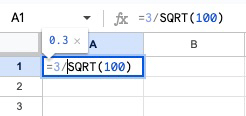
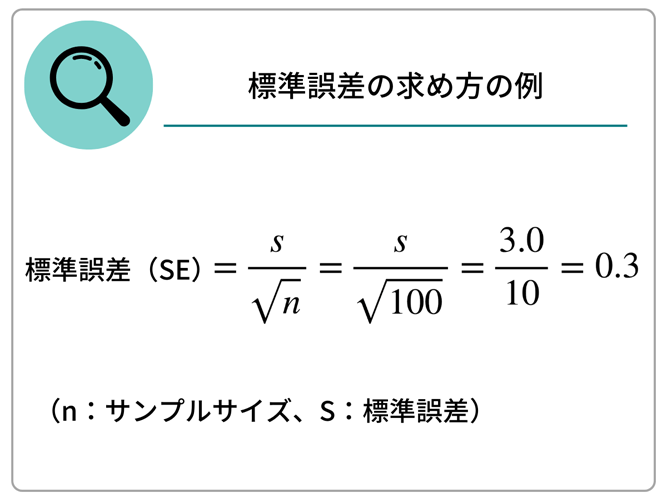
例えば、ある農園で栗100個の重さを図った結果、平均が25.3g、標準偏差3.0gであったとしましょう。すると、標準誤差は以下の式より0.3と導くことができます。

データセットが与えられている場合

標準偏差や平均値が与えられていなくても、データセットが与えられていれば標準誤差の計算は可能です。

例えば、消しゴム10個の重さを量ったところ、それぞれ15.3g、15.9g、15.8g、16.2g、16.3g、16.5g、16.5g、16.9g、16.8g、17.6gであったとします。

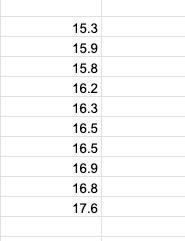
これらのデータから、エクセル関数と分析ツールの基本統計量で、標準誤差を計算する方法を解説しましょう。

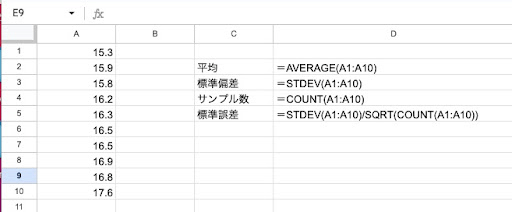
【エクセル関数】

エクセルで、標準偏差（STDEV関数）とサンプル数（COUNT関数）を求め、後は標準誤差を求める式で計算します。

【分析ツール】

エクセルのアドインを用いて、標準誤差を求めることもできます。

▼アドインの追加方法

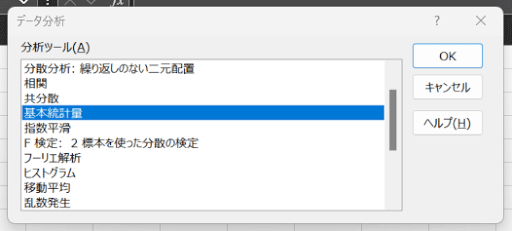
まずは分析ツールのコマンドを選択し、「基本統計量」をクリックします。

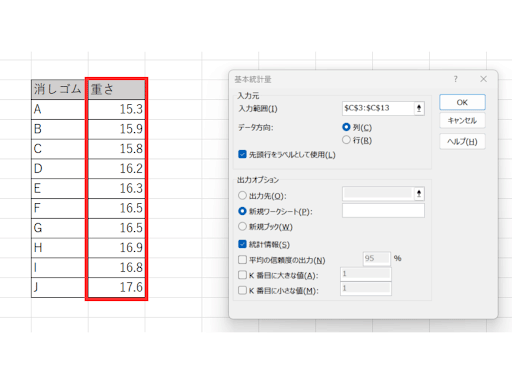
ダイアログボックスが表示されたら、「入力範囲」として求めたい数値部分を選択します。また、「先頭行をラベルとして使用」「統計情報」の2箇所にチェックを入れ、「OK」をクリックします。

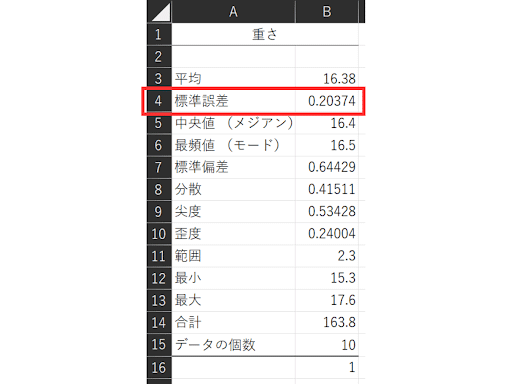
新たなシートに、各統計の数値がまとめて出力され、標準誤差を確認することができます。

まとめ｜標準誤差で、母集団からの標本の誤差を確認できる

標準誤差は、標本から得られる推定量そのもののバラツキです。標準誤差が小さければ小さいほど、標本の調査結果は母集団に近くなります。

正規分布での誤差範囲を決定したり、必要なサンプルサイズを決定する際に活用されることが多い標準誤差。数式だけ見ると一見難しそうに見えますが、エクセルを用いれば簡単に求められるので、ぜひ試してみてください。

よくある質問

Q1.標準偏差と標準誤差の違いは？
標準誤差との大きな違いは、何のバラツキに着目しているかです。 標準偏差はサンプルそのものに着目していますが、標準誤差はサンプルの平均値に着目しています。また、標準誤差は標準偏差をサンプル数の平方根で割っているため、標準誤差より標準偏差が大きくなることはありません。 詳しくは「似ている言葉”標準偏差”とは」の章をご覧ください。
Q2.標準誤差をエクセルで求める方法は？
標準偏差とサンプル数がわかっていれば、そのまま標準誤差を求める計算式に当てはめるだけで計算できます。また、データセットがあれば、数式で算出する方法やアドインでデータ分析を行う方法によって、計算可能です。 詳しくは「標準偏差をエクセルで計算する方法」の章をご覧ください。