交互作用とは?主効果との関係や交互作用の有無を判定するやり方をわかりやすく解説
2022年11月04日

交互作用とは、2つの因子の組合せで初めて現れる相乗効果のことを指します。交互作用のありなしを調べることで、因子同士の因果関係だけでなく、企業活動で重点的にリソースを投下すべきポイントの特定にもつながります。
この記事では、交互作用の意味と主効果の関係、交互作用のありなしを調べるべきシーンなどを解説します。
交互作用とは?
2つの因子の組合せで初めて現れる相乗効果のこと。
交互作用による効果を、交互作用効果と呼びます。
例えば、球場Aにおけるビールの売り上げを調べると、当日の最高気温に加えて年齢層も影響を与えていたとします。
その場合「当日の最高気温」と「年齢層」には相互作用がありこれら2つの因子が「ビールの売り上げ」に交互作用効果を与えていたと言えるのです。
交互作用がある場合のグラフ
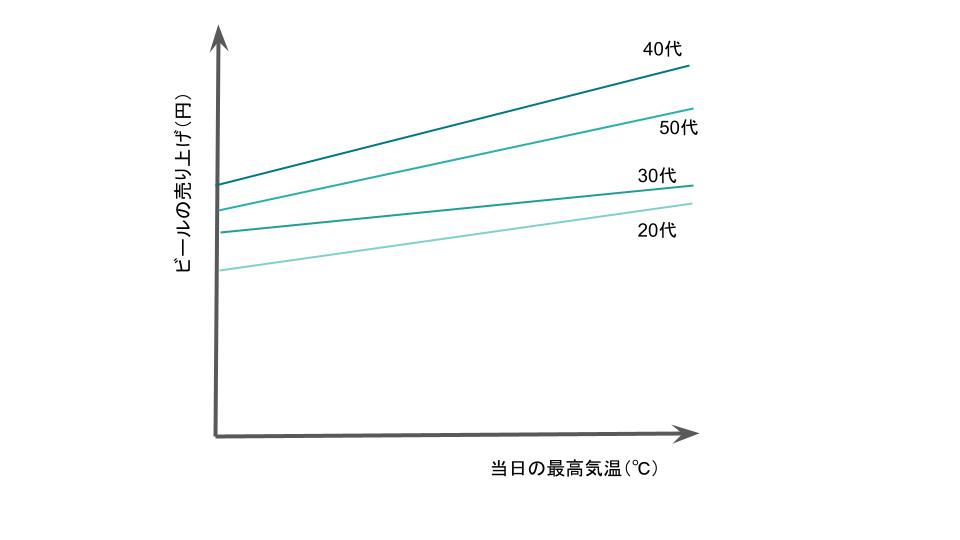
上のグラフでは、球場Aにおいて年齢別(20-50代)に、縦軸にビールの売り上げ(円)、横軸に当日の最高気温(℃)を記載しています。
当日の最高気温と年齢層の間に交互作用があれば、上図の通り年齢別のグラフは平行になりません。
その場合、ビールの売り上げには、当日の最高気温だけでなく年齢層も影響を与えていることになります。
グラフの角度が急になっている年齢層であるほど、当日の最高気温によってビールの売り上げが大きく左右されるのです。
交互作用がない場合のグラフ
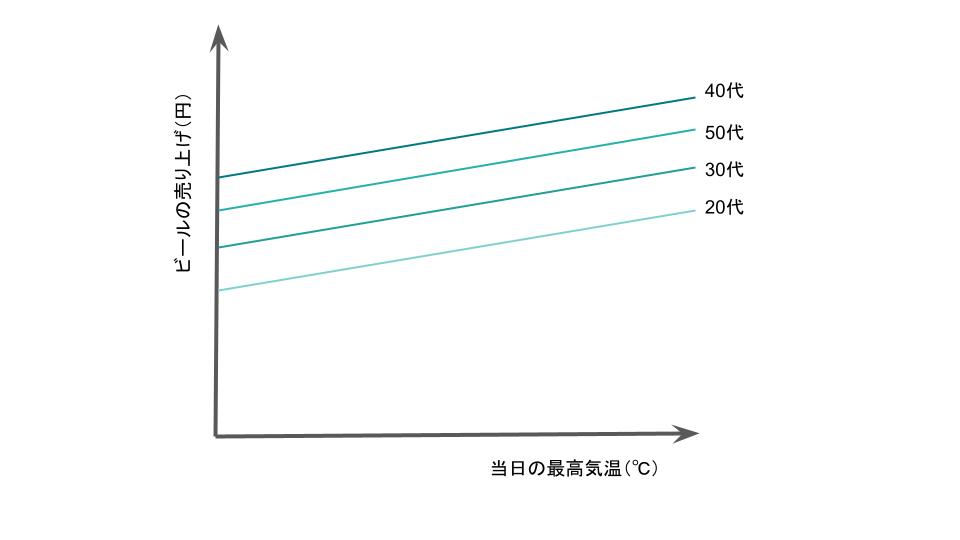
一方、当日の最高気温と年齢層の間に交互作用がなければ、下に示すとおり年齢別のグラフは平行になります。
その場合、ビールの売り上げには、当日の最高気温は影響を与えても、年齢層は影響を与えていないことになります。
そのため、どの年齢層でも、当日の最高気温とビールの売り上げを示すグラフは変わらないのです。
主効果と交互作用の関係
交互作用と関わりが深い用語として「主効果」があります。
それぞれの説明変数が独自に目的変数に与える影響。
交互作用がある場合は、説明変数同士が目的変数に影響を与えることになります。
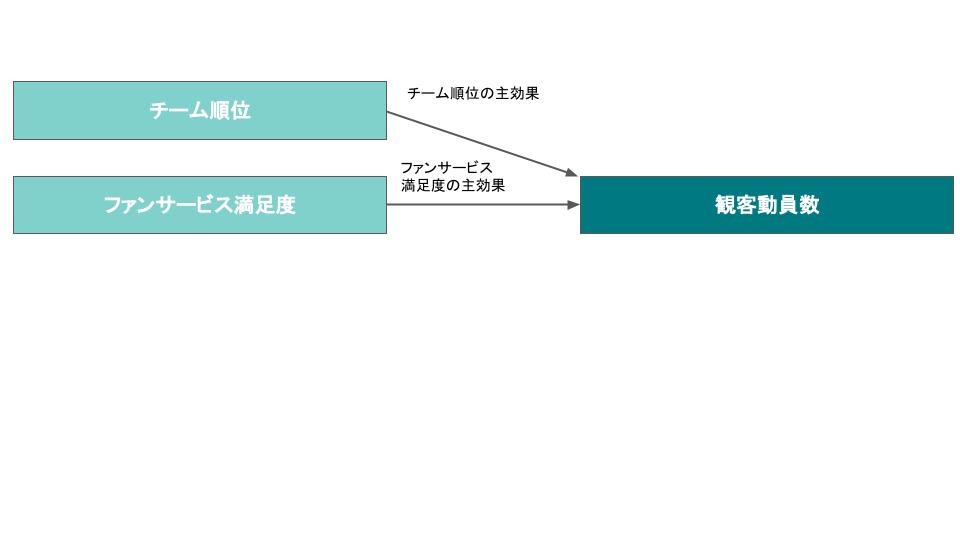
例えば、プロスポーツのスタジアムにおける観客動員数を考えてみましょう。
図に示すとおり、説明変数が「チーム順位」と「ファンサービス満足度」、目的変数が「観客動員数」となります。
また、「チーム順位」と「ファンサービス満足度」は、いずれも主効果として「観客動員数」に影響を与えるのです。
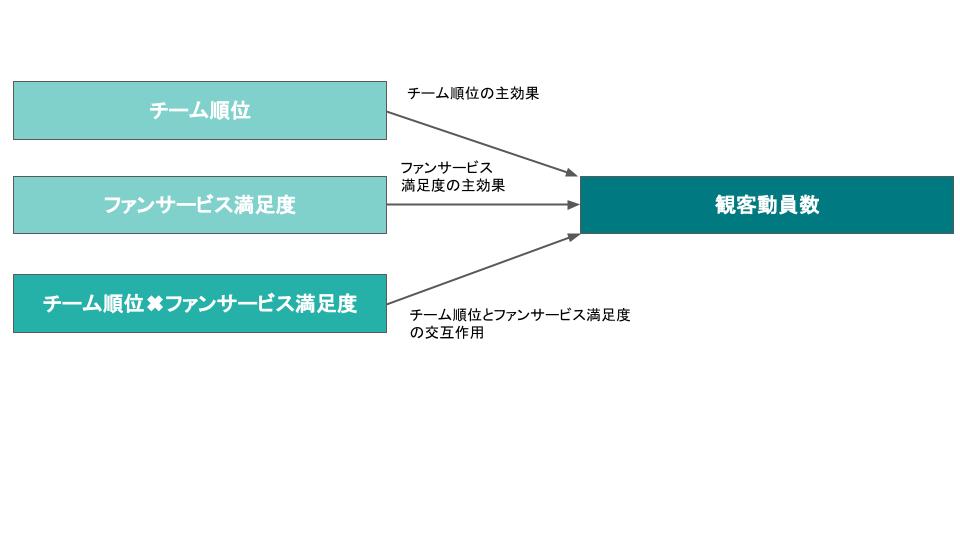
ここで「チーム順位」と「ファンサービス満足度」の交互作用がある場合は「チーム順位」と「ファンサービス満足度」の掛け合わせ(「チーム順位✖️ファンサービス満足度」)も説明変数となり、「観客動員数」に影響を与えることになります。
交互作用のありなしを調べるべきシーン
交互作用のありなしを調べるべきシーンを、2つ解説します。
- 因子同士の詳細な因果関係を調べたい場合
- 重点的に対策を講じるべきポイントを判断したい場合
因子同士の詳細な因果関係を調べたい場合
特定の集団内において、限定的な効果が見受けられる場合、より詳細な内容を調べることで、交互作用を引き起こす要因を特定しやすくなります。
交互作用を引き起こす要因を特定できれば、要因同士の関係性が把握しやすく、改善につながる可能性があります。
例えば、先ほど解説した観客動員数に関する事例で考えてみましょう。
観客動員数には、チーム順位とファンサービス満足度が関係しており、両者に相互作用がある場合、チーム順位が低いチームではファンサービス満足度が低下すると考えられます。
そのため例えば、実績のある選手・指導者の獲得やスコアラーの増員など、チーム力を向上させてチーム順位を上げることで、ファンサービス満足度向上も期待できるでしょう。
反対に、球場でのイベントやSNSによる情報発信など、ファンサービス満足度を向上させることで、結果的にチーム順位アップにもつながると期待できます。
重点的に対策を講じるべきポイントを判断したい場合
企業活動においては、人員や予算などのリソースに制限がある場合がほとんどです。
交互作用のありなしを調べることで、売上や稼働時間など、重点的に対策を講じるべきポイントを判断しやすくなります。その結果、限られたリソースを効率的に投下しやすくなり、よりよい企業活動につながります。
具体例をあげると、採用促進のためにSNSアカウントを運用しているとします。
SNSアカウントを分析した結果、地方在住でフルリモート勤務希望の転職希望者向け投稿が伸びていたら、その内容を中心に投稿することが効果的と考えられます。
他にも改善したい指標に対して悪影響を与える因子を特定できれば、介入しない方がいいと判断できる場合もあります。
例えば新卒採用では好評だったカジュアル面談が、40代以上向けの中途採用ではかえって評判を下げる結果になったとします。
この場合、40代以上向けの中途採用向けには、カジュアル面談を行わない方がよいと考えられるでしょう。
交互作用のありなしを判定する分析手法
では最後に交互作用のありなしを判定する分析手法を2つ解説します。
- 分散分析
- 重回帰分析
分散分析
分散分析とは、複数(3群以上)データ群の平均値が、統計学的に有意な差があるか判定する分析手法のことで、ANOVA(Analysis of Variance)とも呼ばれます。
交互作用の有無を知りたい場合は、要因同士の関係を明らかにするため、二元配置分散分析を用いましょう。
二元配置とは、グループを識別する要素が複数存在するデータ(例:足の速さについて、国籍と身長を用いてグループ分け)を意味します。グループを識別する要素が1つしか存在しないデータ(例:足の速さについて、国籍でグループ分け)は、一元配置と呼びます。
▼関連記事
有意差とは?帰無仮説/対立仮説の考え方とビジネスでの活用を解説 | リサーチコラム
重回帰分析
重回帰分析とは、結果(目的変数)を予測する際に、2つ以上の変数(説明変数)との相関関係を数式化して示す統計分析手法のことです。
各説明変数における目的変数への影響度を、具体的な数値で算出できます。
▼関連記事
重回帰分析とは?ビジネスでの活用シーンや方法・注意点を解説 | リサーチコラム
まとめ
ここまで交互作用の概要や、交互作用のありなしを調べるべきシーンを解説しました。企業活動で活用できるリソースには限りがあるので、交互作用のありなしを判定し効果的にリソースを投下できれば、よりよい企業活動につながるでしょう。
ぜひこの記事を参考に、交互作用のありなしを調べてみてはいかがでしょうか。
- サービス概要を無料配布中「3分で読めるGMOリサーチ&AIのサービス」
-
GMOリサーチ&AIはお客様のマーケティング活動を支援しており、さまざまなサービスを提供しております。
- スピーディーにアンケートデータを収集するには
- お客様ご自身で好きな時にアンケートを実施する方法
- どこの誰にどれくらいリーチができるか
ぜひこの機会にお求めください。 - 資料請求する


